Para encontrar un punto intermedio en una recta, recurriremos al concepto de razón ($r$) y que es solamente una porción de la recta sobre el resto de ella. Para entender esto recurriremos a la siguiente figura:

Como vemos en la figura anterior, si deseo saber cual es la razón ($r$) del punto P(x,y), debo dividir la distancia de A hasta P $=\overline{AP}$ entre la distancia de P hasta B $=\overline{PB}$.
Lo podemos pensar de dos formas, una contando la distancia $\overline{AP}$ que es igual a 2 y de $\overline{PB}$ que es igual a 4, la otra es ver que en la distancia $\overline{AB}$, se puso en tres partes (número azules) y que de $\overline{AP}$ le corresponde una parte y de $\overline{PB}$ le corresponde dos partes, de cualquier forma nos daría el mismo resultado como veremos a continuación.
$$r=\frac{\overline{AP}}{\overline{PB}}$$
En nuestro caso sustituyendo los valores de la figura
$$r=\frac{\overline{AP}}{\overline{PB}}=\frac{2}{4}$$
Lo anterior reduciendo la fracción queda:
$$r=\frac{1}{2}$$
Si se ve en la figura , el punto se encuentra a una tercera parte de la distancia entre la logitud $\overline{AB}$, pero la razón no es igual a 1/3, sino a 1/2, porque la definión nos dice que es una división entre la distancia del punto inicial al punto P entre la distancia del punto P al punto final.
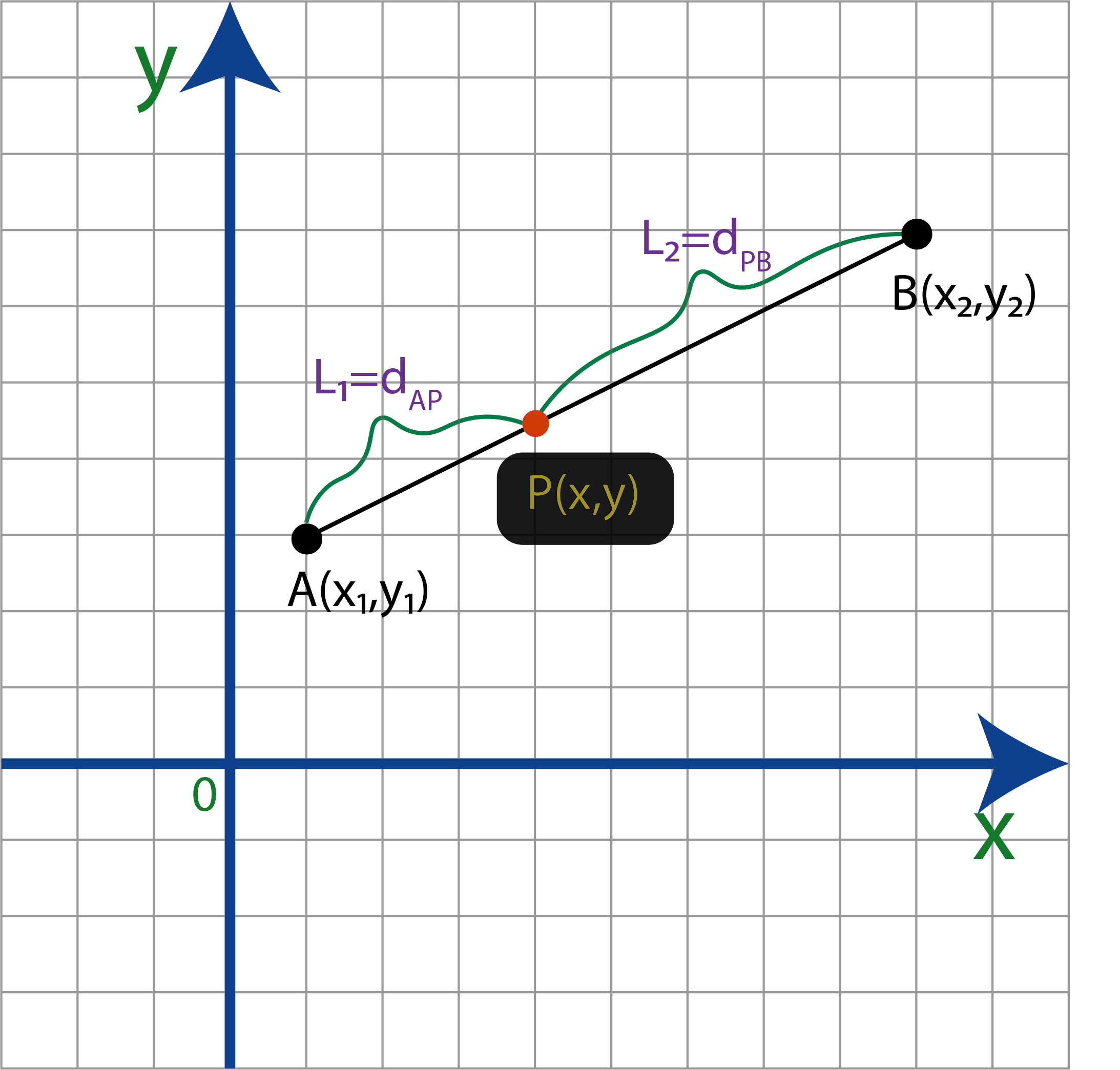
Para tener una definición concreta del concepto, decimos que una razón dada es la división entre dos longitudes $L_1$ y $L_2$ de una recta cuyos extremos son los puntos $A(x_1,y_1)$ y $B(x_2,y_2)$. La división anterior nos ayuda a encontrar puntos intermedios sobre una recta.
Para revisar lo anterior nos basaremos en la siguiente figura:

Como vemos en la figura hay una recta que va desde el punto A hasta el B y queremos encontrar un punto en alguna parte de ella. Para esta recurrimos a la razón dada por el punto P(x,y). La fórmula es la siguiente:
$$r=\frac{L_1}{L_2}=\frac{d_{AP}}{d_{PB}}$$
Para encontrar la coordenada $P(x,y)$, recurriremos a las siguientes ecuaciones que salen de los puntos $A(x_1,y_1)$, $B(x_2,y_2)$ y la razón $r$:
$$x=\frac{x_1+x_2r}{1+r}$$ $$y=\frac{y_1+y_2r}{1+r}$$
A partir de esta fórmula podemos encontrar la coordenada $P(x,y)$ donde se encuentra la razón dada sobre la recta.
Ejemplo de división de un segmento de una recta en una razón dada.
Determinar el punto $P(x,y)$ que está a la tercera parte del camino entre A(2,5) y B(8,-1)
Solución:
En la figura 1 vemos que la razón para una tercera parte de una distancia es $r=\frac{1}{2}$
Por lo tanto, introducimos esos valores en las ecuaciones para x e y.
$$x=\frac{x_1+x_2r}{1+r}$$ $$y=\frac{y_1+y_2r}{1+r}$$
$$x=\frac{2+(8)(\frac{1}{2})}{1+\frac{1}{2}}=\frac{2+(\frac{8}{2})}{\frac{2}{2}+\frac{1}{2}}$$
$$x=\frac{2+4}{\frac{3}{2}}$$
$$x=\frac{6}{\frac{3}{2}}=\frac{\frac{6}{1}}{\frac{3}{2}}$$
$$x=\frac{12}{3}=4$$
$$x=4$$
$$y=\frac{5+(-1)(\frac{1}{2})}{1+\frac{1}{2}}$$
$$y=\frac{5+(\frac{-1}{2})}{\frac{3}{2}}=\frac{\frac{10}{2}+(\frac{-1}{2})}{\frac{3}{2}}$$
$$y=\frac{\frac{9}{2}}{\frac{3}{2}}=\frac{9}{3}$$
$$y=3$$
El resultado se puede expresar de la siguiente forma:
El punto $P(4,3)$ es la coordenada que se encuentra a un tercera parte sobre la recta $\overline{AB}$
Punto medio de una recta.
Una de las aplicaciones de la razón es encontrar un punto medio de una longitud, por lo tanto vamos a encontrar una ecuación para determinar el punto medio de una recta.
Si tenemos una distancia y ubicamos su punto medio, sabemos que del punto inicial de la distancia al punto medio y del punto medio al punto final tienen la misma distancia. Por lo tanto, podemos decir que la razón para un punto ubicado a la mitad es uno ($r=1$).
Partiendo de que $r=1$ y llevándolo a nuestras ecuaciones para encontrar los valores de x e y, tenemos lo siguiente:
$$x=\frac{x_1+x_2(1)}{1+(1)}$$
$$x=\frac{x_1+x_2}{2}$$
$$y=\frac{y_1+y_2(1)}{1+(1)}$$
$$y=\frac{y_1+y_2}{2}$$
Si la ponemos en forma de coordenada queda lo siguiente:
$$PM\left( \frac{x_1 + x_2}{2},\frac{y_1 + y_2}{2} \right)$$
Ejemplo de Punto Medio.
Determinar el punto que se encuentra a la mitad de los puntos A(3,5) y B(9,-7).
Las coordenadas de los puntos anteriores se introducen en nuestra fórmula de punto medio y queda de la siguiente forma:
$$PM\left( \frac{3 + 9}{2},\frac{5 + (-7)}{2} \right)$$
$$PM\left( \frac{12}{2},\frac{-2}{2} \right)$$
El punto que se encuentra a la mitad de A y B es $PM( 6,-1). $