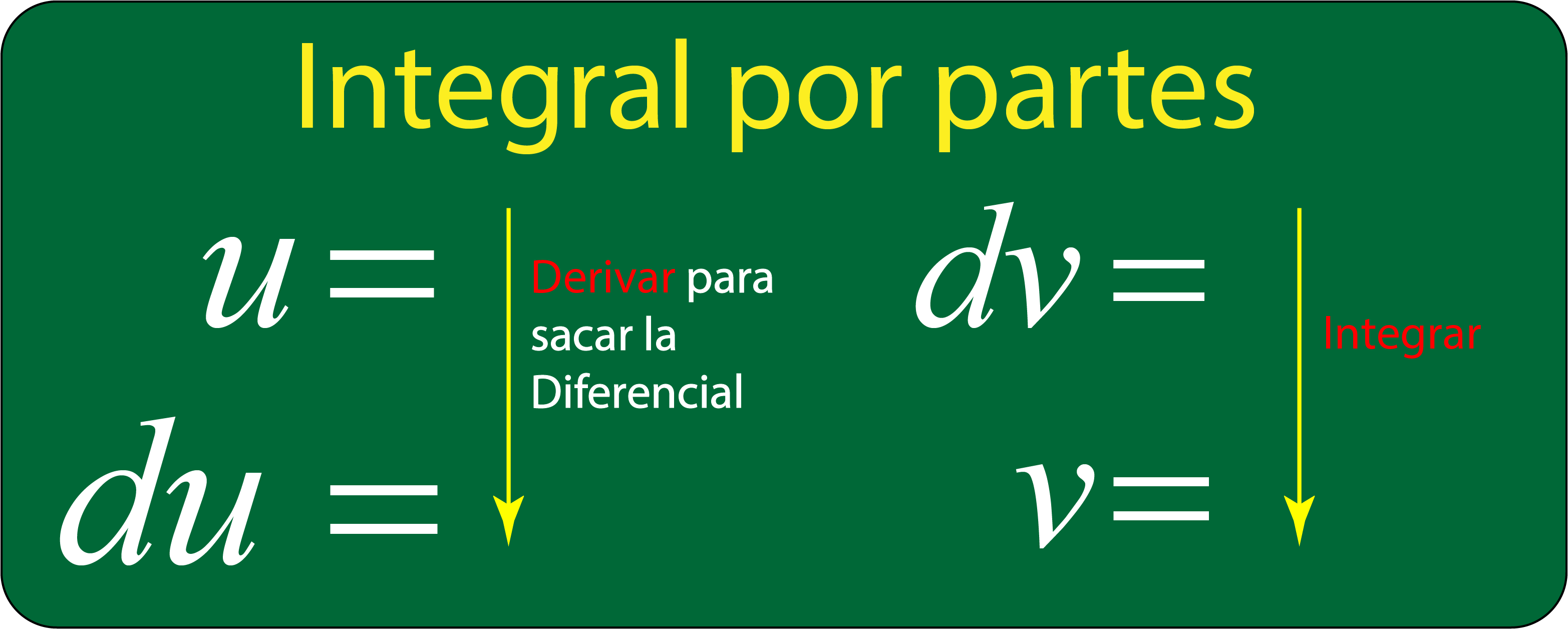
El método integral por partes se da con la siguiente integral:
$$\int {u\;dv = uv – \int {v\;du} } $$
el método nos dice que tenemos que encontrar primero
una $$u$$ y después una $$dv$$
Revisemos el siguiente ejemplo:
$$\int{x\sin\;x\;dx}$$
para este ejemplo de integral por partes, debemos establecer cuanto vale $$u$$,
en este caso será $$x$$ y $$dv$$ será $$\sin x$$
| $$u=x$$ | $$dv=\sin x$$ |
| $$du=\;dx$$ | $$v=-cos x$$ |
Por lo tanto la solución por medio de la fórmula
$$\int {u\;dv = uv – \int {v\;du} } $$ es:
$$= -x \;cos\; x-\int{-cos\;x\;dx}$$
integrando $$-\int{-cos\;x\;dx}$$ nos da como resultado lo siguiente
$$= -x \;cos\; x + sin\;x+C$$
Ejercicio 2
Realizar $$\int x\root 3\of{x-3}\; dx$$
| $$u=x$$ | $$dv=\root 3\of{x-3}$$ |
| $$du=\;dx$$ | $$\color{blue}{v = \frac{3}{4}{\left( {x – 3} \right)^{4/3}}}$$ |
Para determinar a la letra$$v$$ se debe cambiar de $$dv=\sqrt{x-3}$$
por $$dv=(x-3)^{\frac{1}{3}}$$ e integrarla
Siendo
| $$w=x-3$$ | $$dw=dx$$ |
Estando completa la integral, se precederá a cambiarla de variable, quedando de la siguiente forma
$$\int w^{\frac{1}{3}}dx$$
Resolviendo la anterior integral
$$=\frac{3}{4}{\left( {w} \right)^{4/3}}$$
Cambiando la variable $$w$$ por su valor original, queda de la siguiente forma
$$\color{blue}{v=\frac{3}{4}{\left( {x – 3} \right)^{4/3}}}$$
Ahora teniendo los datos completos , procedemos a aplicar la fórmula de integral por partes
$$\int {u\;dv = uv – \int {v\;du} } $$
Lo cual queda
$$=\frac{3}{4}x{\left( {x – 3} \right)^{4/3}} – \frac{3}{4}\int {(x – 3)^{4/3}}dx$$
Por último procedemos a calcular la integral resultante, por cambio de variable
$$z=(x – 3)$$ y $$dz=dx$$
Estando completa la función, tenemos:
$$\int z^{\frac{4}{3}}\;dz=\frac{3}{7}{\left( {z} \right)^{7/3}}$$
Cambiando la variable $$z$$ queda
$$\frac{3}{7}{\left( {x – 1} \right)^{7/3}}$$
y poniéndola en la integral resultante nos da
$$=\frac{3}{4}x{\left( {x – 3} \right)^{4/3}} – \frac{3}{7}{\left( {x – 1} \right)^{7/3}}+C$$
lo cual es el Resultado