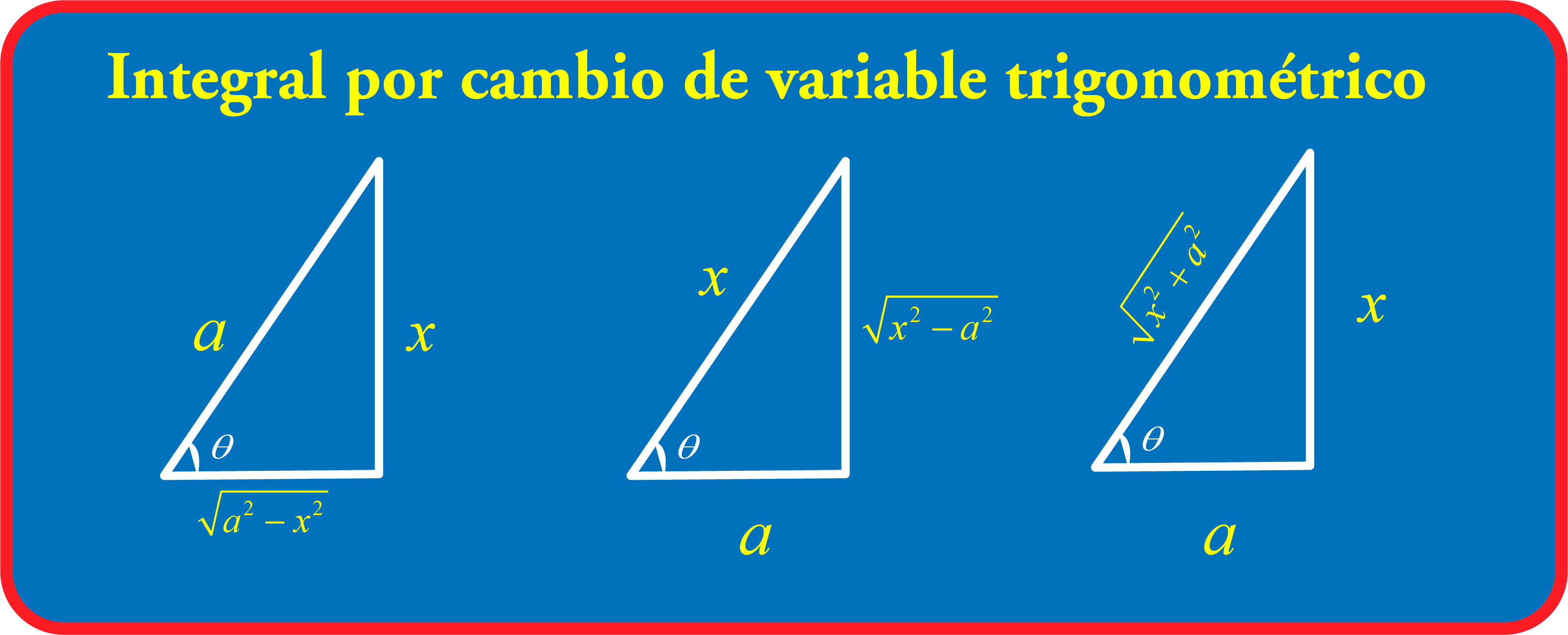
En el método de integral cambio de variable trigonométrico se da mediante unos triángulos
que relacionan funciones trigonométricas
Se puede uno guiar con los triángulos de la figura anterior.
Más adelante veremos ejemplos de cada uno de los tres casos de cambio de variable trigonométrico.
Ejercicio Caso 1
Ejemplo 1 integral cambio de variable trigonométrico
Realizar la siguiente integral
$$\int\;{{x\;dx}\over{\sqrt{4-x^2}}}$$
De acuerdo a la figura tenemos lo siguiente

del triángulo debemos determinar $$x$$, $$dx$$ y la raíz cuadrada.
Comenzaremos por la letra x
$$\sin {\rm{\theta }} = \frac{{\rm{x}}}{{\rm{a}}}$$
Despejando la letra x. obtenemos
\[{\rm{x}} = 2\sin {\rm{\theta }}\]
Ahora lo anterior le determinamos su diferencial
\[dx = 2\cos \theta {\rm{ }}\;d\theta \]
Lo siguiente será determinar el valor de la raíz cuadrada y eso se hará con la función coseno, quedando :
\[\cos \theta = \frac{{\sqrt {{a^2} – {x^2}} }}{a}\]
Despejando la raíz cuadrada, queda de la siguiente forma
\[\sqrt {4 – {x^2}} = 2\cos \theta \]
El siguiente paso será hacer el cambio de variable por las funciones trigonométricas resultantes anteriormente
\[\int {\frac{{2sin\theta \;2\cos \theta \;d\theta }}{{2\cos \theta }}} \]
Reduciendo , llegamos a una integral sencilla
$$=2\int\sin\theta$$
Quedando el resultado trigonométrico
\[ = – 2\cos \theta + C\]
Por último se tiene que hacer el cambio a la forma inicial de la integral, donde sabemos que $$\cos \theta= \frac{{\sqrt {{4} – {x^2}} }}{2}$$
Lo anterior sustituyéndolo en el resultado trigonométrico
\[ = – 2\left[ {\frac{{\sqrt {{\rm{4}} – {{\rm{x}}^2}} }}{2}} \right] + C\]
y el resultado final queda
$$= – \sqrt {4 – {{\rm{x}}^2}} + C$$