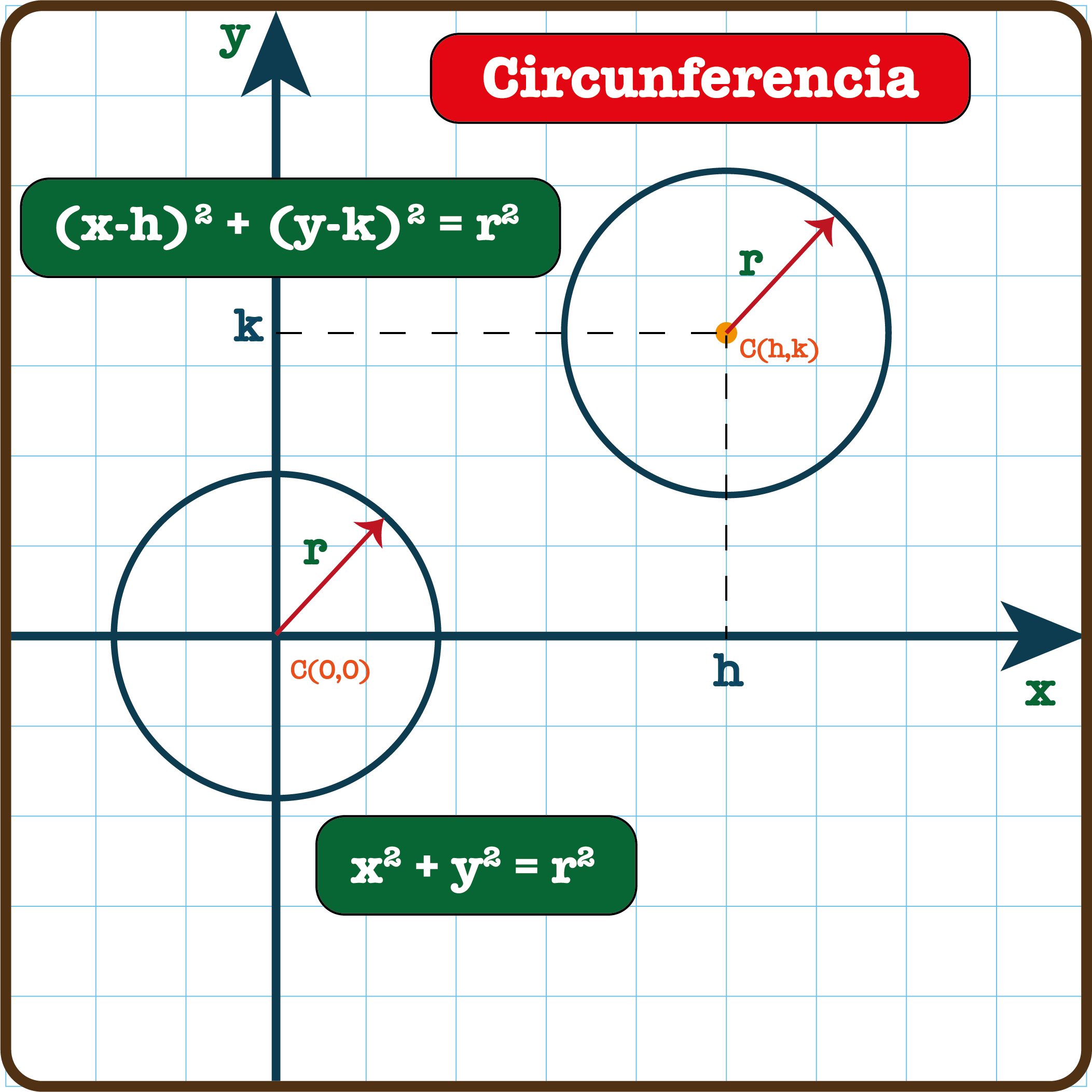
Circunferencia con centro en el origen

“Una circunferencia es el lugar geométrico de los puntos de un plano que equidistan a otro punto llamado centro. Por lo tanto, es una figura que debemos estudiar en nuestro curso, dado que se encuentra en el plano cartesiano. Hay dos tipos de ecuaciones en nuestro temario de geometría analítica, una es la de centro en el origen y la otra con centro fuera del origen. Nota tomada de Wikipedia.

La ecuación con centro en el origen se tiene la siguiente ecuación:

Con la ecuación anterior podemos determinar muchos características de la circunferencia como es su área, perímetro, radio, diámetro entre otras.

Ejemplo de circunferencia con centro en el origen.

Determinar la ecuación de la circunferencia con centro en el origen que contiene al punto $P(4,2)$ , así como también el área y perímetro.

Lo primero que debemos calcular para la ecuación de la circunferencia con centro en el origen es el radio, mismo que nos servirá tanto para el área como para el perímetro.

Como sabemos que el centro está en el origen $C(0,0)$ , tomamos la distancia del centro al punto $P(4,2)$ , con la fórmula de distancia entre dos puntos.

$$d_{cp}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
$$d_{cp}=\sqrt{(4-0)^2+(2-0)^2}$$
$$d_{cp}=\sqrt{(4)^2+(2)^2}=\sqrt{16+4}$$
$$r=d_{cp}=\sqrt{20}$$
$$r=\sqrt{20}\;u$$

El radio en la ecuación de la circunferencia lo pide al cuadrado, por lo tanto, tenemos lo siguiente:

$$r=\sqrt{20}$$
$$(r)^2=(\sqrt{20})^2$$
$$r^2=20$$

Y puesto en la ecuación de la circunferencia con centro en el origen es $x^2+y^2=r^2$ y sustituyendo $r^2=20$, queda de la siguiente forma:

Para calcular en perímetro utilizaremos la fórmula $P=2\;\pi \;r=\;\pi \;d$ y sustituimos el radio.

$$P=2\;\pi \;r=2\;\pi \;(\sqrt{20})$$
$$P=2\;\sqrt{20}\;\pi=28.1\;u $$

Para el área, se sutituye el radio en la fórmula.

$$A=\pi\;r^2=\pi\;(\sqrt{20})^2$$
$$A=(20)\pi\;=62.8\;u^2$$

Circunferencia con centro fuera del origen.

Para la circunferencia que su centro se ubica fuera del origen tenemos la siguiente ecuación.

De la ecuación anterior podemos determinar la coordenada del centro $C(h,k)$ y su radio $r$.

Ejercicio de circunferencia fuera del origen

Sean A(1,1) y B(5,3) los extremos del diámetro de una circunferencia, determinar su ecuación en forma ordinaria.

Primero debemos calcular su punto medio entre los puntos A y B.

$$PM_{AB}=\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)$$
$$PM_{AB}=\left(\frac{1+5}{2},\frac{1+3}{2}\right)$$
$$PM_{AB}=\left(\frac{6}{2},\frac{4}{2}\right)$$
$$PM_{AB}=\left(3,2\right)$$

Teniendo el punto medio y sabiendo que es igual al centro $C(3,2)$, procederemos a calcular el radio, podemos resolverlo de dos formas, una sacando la distancia de A hasta B y dividiéndola entre dos, dado que la distancia entre A y B es el diámetro o calculando la distancia de C hasta A, dado que esa es la distancia del centro hasta un punto de la circunferencia y por tanto es su radio.

Calcularemos la distancia de A hasta C.

Ponemos como $x_1=1$, $y_1=1$, $x_2=3$ e $y_2=2$ dentro de la siguiente ecuación.

$$d_{AC}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$$
$$d_{AC}=\sqrt{(3-1)^2+(2-1)^2}$$
$$d_{AC}=\sqrt{(2)^2+(1)^2}$$
$$d_{AC}=\sqrt{4+1}$$
$$r=d_{AC}=\sqrt{5}$$

Para nuestra ecuación necesitamos el radio y las coordenadas del centro

$r=\sqrt{5}$ y $C(3,2)$, lo sustituimos en la ecuación de la circunferencia con centro fuera del origen y nos queda:

$$(x-h)^2+(y-k)^2=r^2$$
$$(x-3)^2+(y-2)^2=(\sqrt{5})^2$$