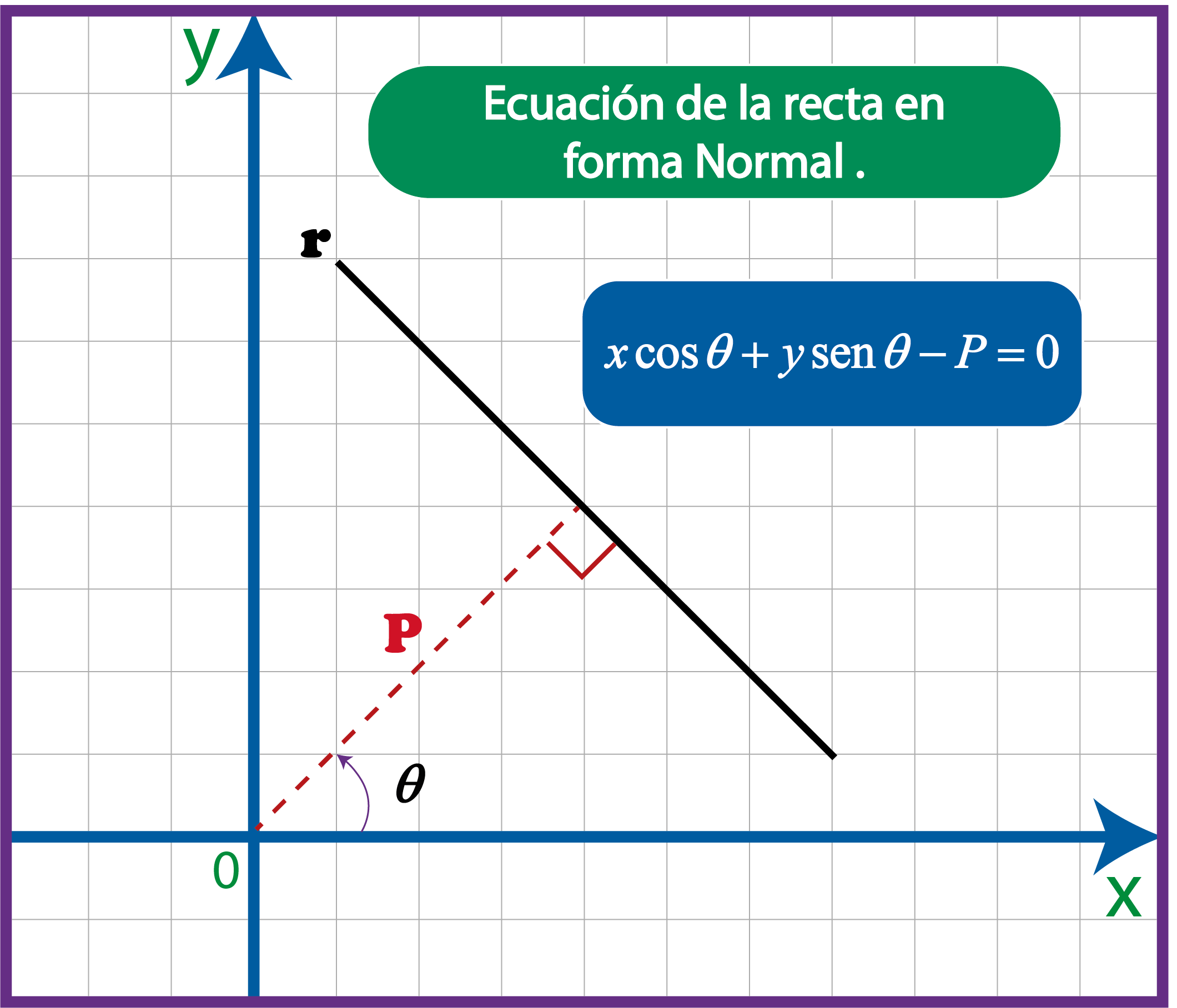
La ecuación de la recta en forma normal nos propociona el ángulo $\theta$ de una recta que sale desde el origen, así como su longitud (P ) hasta una recta r que esta a 90°, ver la figura anterior.
La ecuación que se utiliza es la siguiente:
Ejemplo de ecuación de la línea recta en forma normal.
Calcular la ecuación de la recta en forma normal si P=9 y $\theta=45°$
Solución: Sabemos que la ecuación necesita del valor de P y de $\theta$ por lo tanto sustituimos los valores en la ecuación normal de la recta como se muestra a continuación.
$$x\;cos\;45°+y\;sen\;45°-9=0$$
Para entregar un resultado correcto y completo recurriremos a que $cos \;45°=\frac{\sqrt{2}}{2}$ y $sen \;45°=\frac{\sqrt{2}}{2}$, por lo tanto tenemos:
<
Reducción de la ecuación de la recta de la forma general a la normal.
Se deben tener consideraciones, dado que existe una raíz cuadrada en el denominador de cada término.
Primera consideración. Debemos tomar el signo contrario al del valor de $C$ en la raíz $\sqrt {{A^2} + {B^2}}$
Segunda consideración. En caso de que $C=0$, el signo de la raíz $\sqrt {{A^2} + {B^2}}$ es igual al del signo del coeficiente de y, llamado $B$.
Ejemplo de transformación de ecuación general a normal.
Reduce la ecuación $6x-3y-7$ a la forma normal.
Se nota en la ecuación que el valor de $C$ es negativo, por lo tanto, el valor de $\sqrt {{A^2} + {B^2}}$ debe ser positivo (primera consideración).
Lo primero que debemos calcular es el valor de la raíz $\sqrt {{A^2} + {B^2}}$
$$\sqrt {{A^2} + {B^2}}=\sqrt {{(6)^2} + {(-3)^2}}$$
$$\sqrt {36 + 9}=\sqrt {45}$$
Como se había dicho antes, el valor de la raíz es positivo , por lo tanto queda de la siguiente forma:
Esta es la ecuación de la recta en forma norma l, partiendo de una ecuación en forma general.