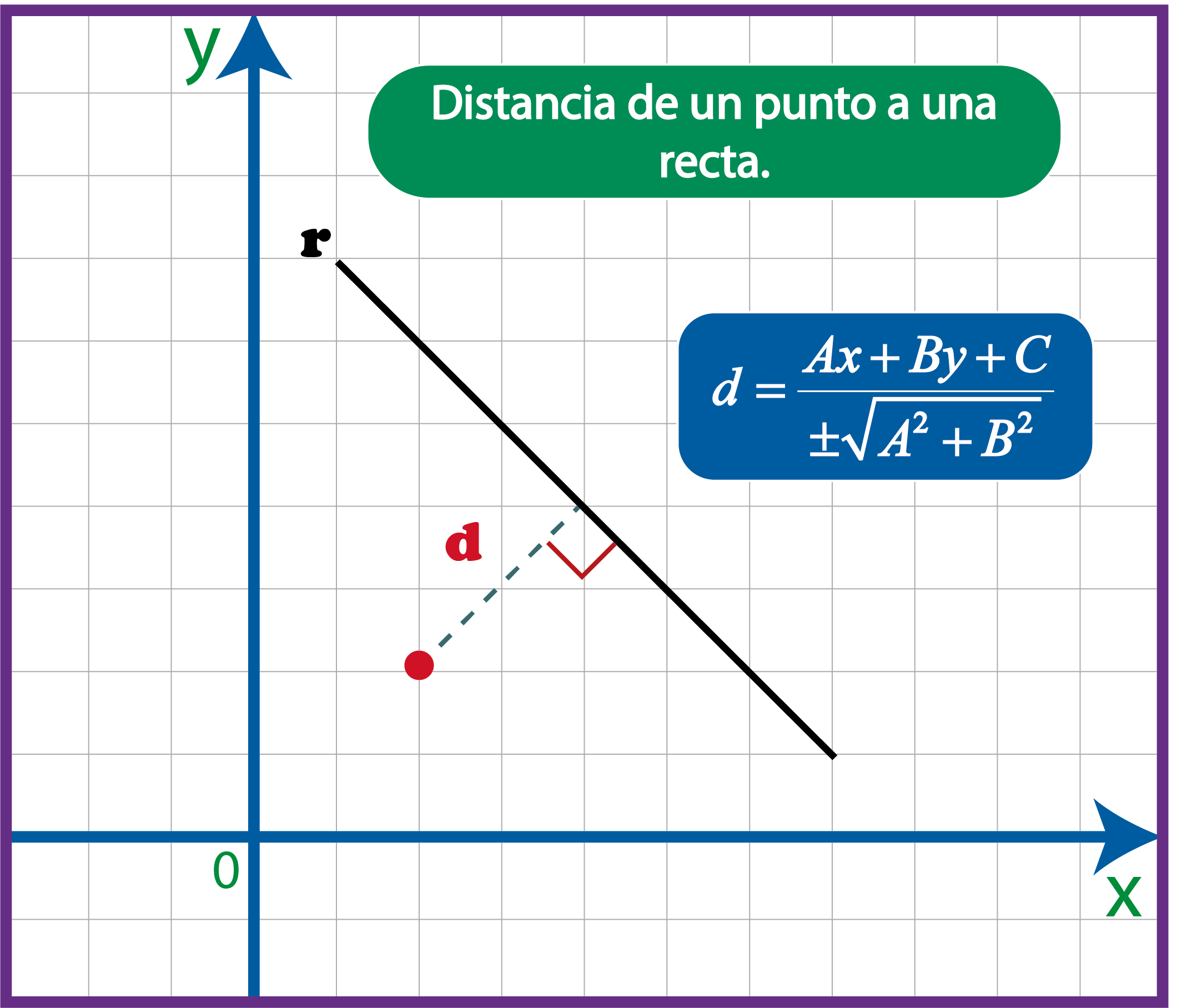
La distancia de un punto a una recta se calcula con la siguiente fórmula:
De acuerdo a la fórmula,la distancia puede ser negativa o positiva, para saber que valor debe tomar, dado que la raíz cuadrada tiene el valor $\pm$, debemos considerar varias cosas.
Consideraciones
La distancia $d$ es positiva si el punto $R(x_1,y_1)$ está por arriba de la recta y negativo si se encuentra abajo de ella.
De la ecuación $Ax+By+C=0$, con B mayor que cero y un punto conocido $(x_0,y_0)$, está arriba de la recta si a la hora de hacer la sustitución de $x_0$ por $x$ y $y_0$ por $y$ en la ecuación $Ax+By+C=0$ resulta una cantidad positiva y se considerará que se sitúa debajo de la recta si el valor encontrado es negativo.
Si el valor de la letra B es negativo, solo se tiene que multiplicar por $(-1)$ ambos lados de la ecuación $Ax+By+C=0$ y se hará lo dicho en el punto anterior.
Ejemplo de distancia de un punto a una recta.
Calcular la distancia del punto $P(2,1)$ a la recta $3x+10y-64=0$.
Primero determinaremos si la distancia es positiva o negativa, para esto debemos sustituir el valor de $P(2,1)$ en la ecuación $3x+10y-64=0$ y ver que B es positivo.
$$3(2)+10(1)-64=-48$$
Lo anterior determina que el punto está debajo de la línea y será una distancia negativa
Viendo por otroa parte el signo, el valor de la raíz lo determina el valor de la letra B, es decir, si la B es positiva, la raíz también lo es, de lo contrario la raíz tomará el signo negativo.
Sustituyendo los valores, tenemos que:
$$d=\frac{3(2)+10(1)-64}{+\sqrt{3^2+10^2}}$$
$$d=\frac{-48}{+\sqrt{9+100}}$$
$$d=\frac{-48}{+\sqrt{109}}$$