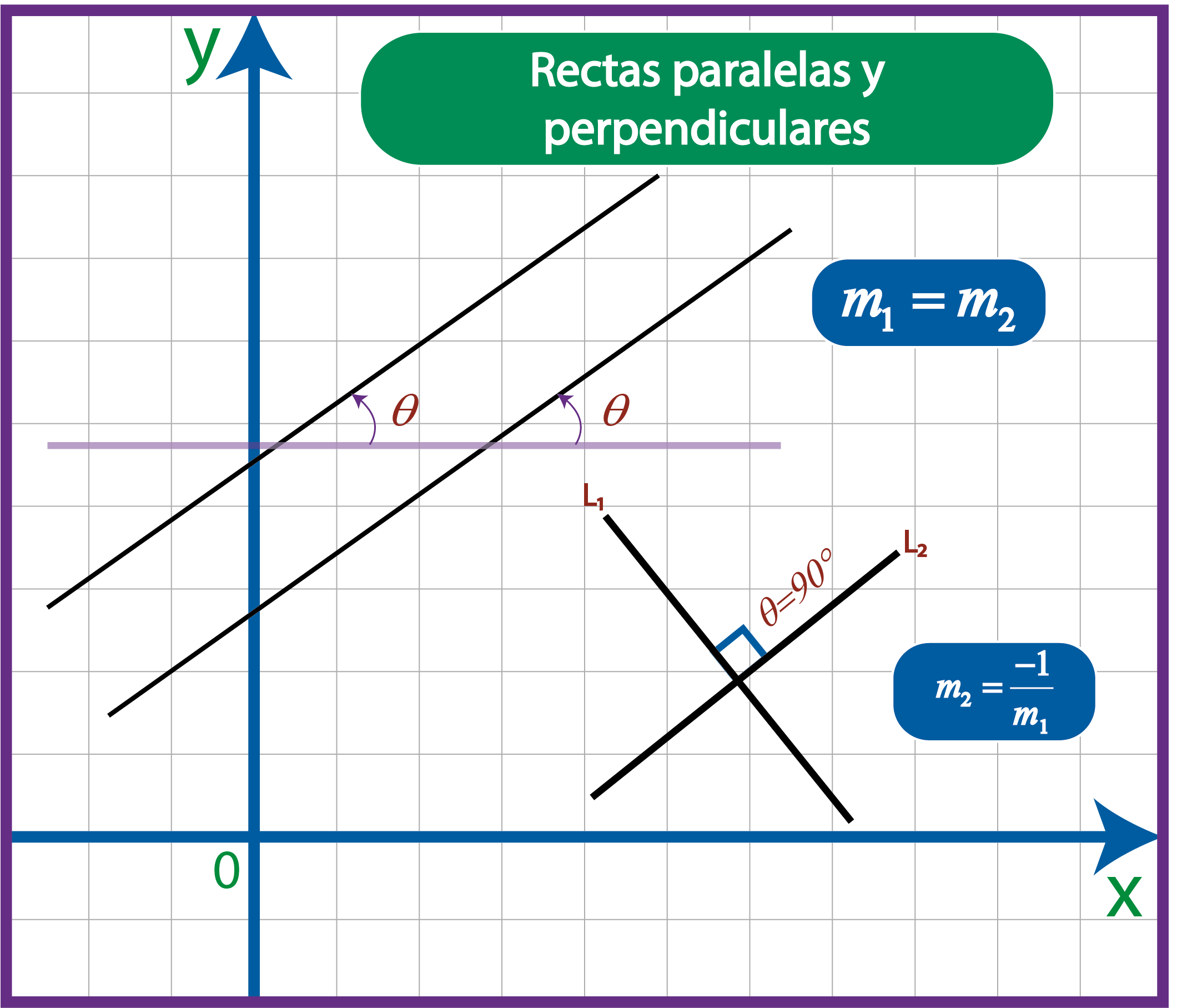
Dentro de las diferentes aplicaciones que tiene la pendiente podemos descubrir el paralelismo y la perpendicularidad de una recta con la otra.
De acuerdo al diccionario de la lengua española, paralelo(a) es “Dicho de dos o más líneas o superficies: Que al ser equidistantes entre sí, por más que se prolonguen nunca pueden encontrarse.” y dentro de la Geometría Analítica se puede saber si dos líneas rectas son o no paralelas.
Pendientes de dos líneas paralelas.
- Dos líneas no verticales con la misma pendiente son paralelas
- Dos líneas paralelas no verticales tiene la misma pendiente
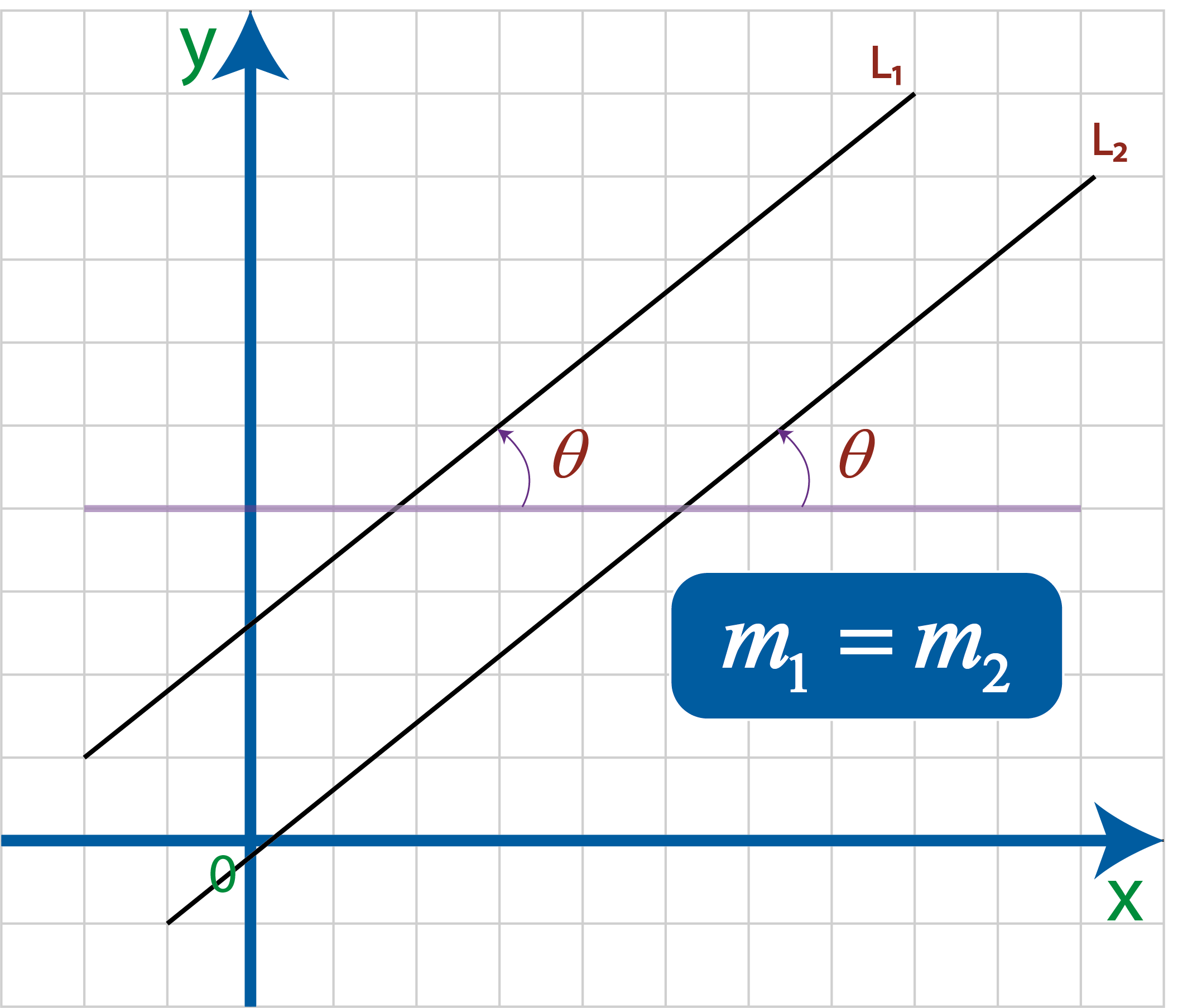
De acuerdo a la figura anterior, podemos ver que si tenemos dos rectas y éstas son paralelas, entonces sus pendientes son iguales.
Pendientes de dos líneas perpendiculares.
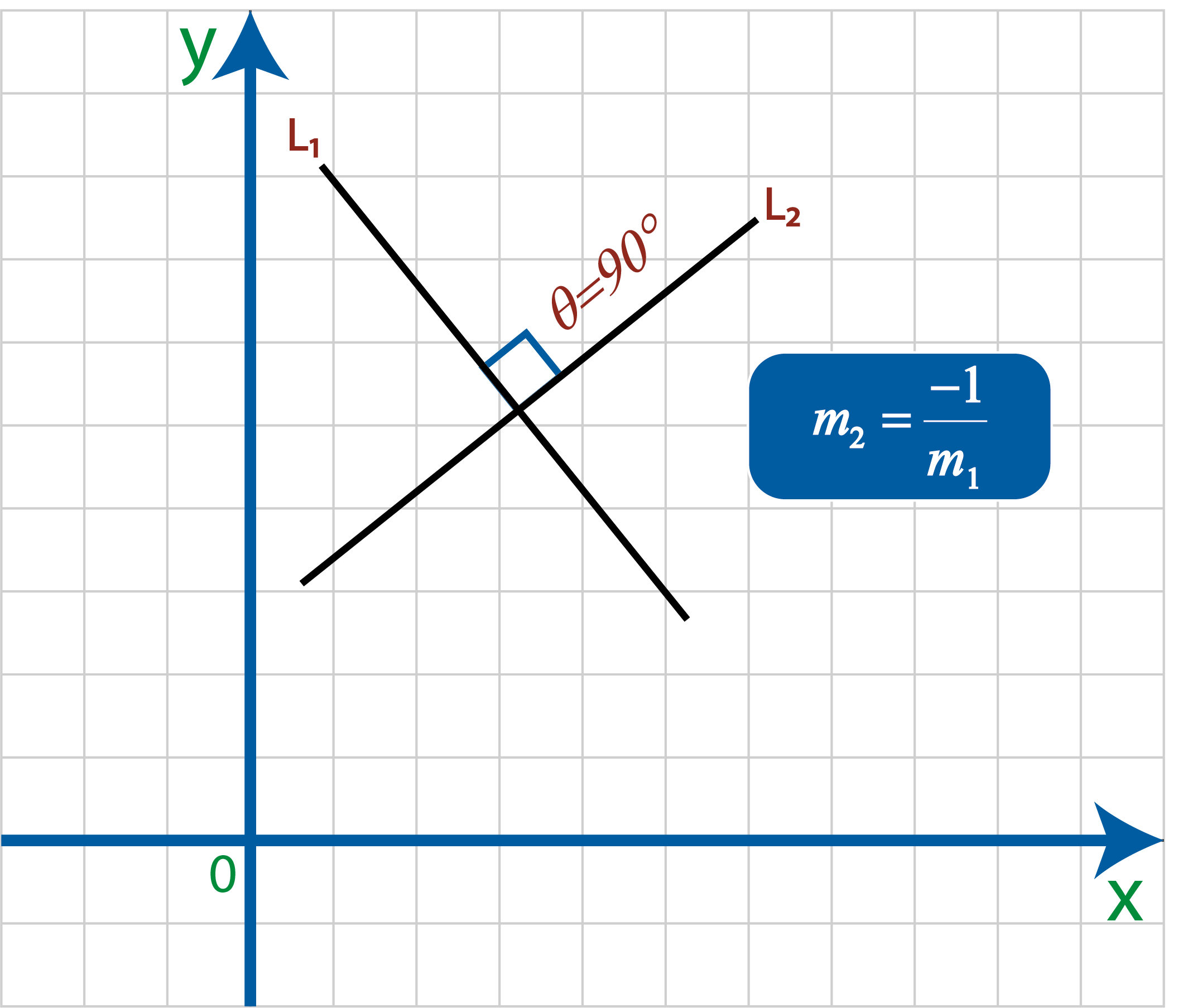
Para saber si dos rectas son perpendiculares, debemos obtener el valor recíproco negativo de una de las pendientes y si da igual en valor a la otra pendiente diremos que las rectas son perpendiculares.
$$m_1=\frac{-1}{m_2}$$
también se puede ver de la siguiente forma:
$$m_1\;m_2=-1$$
Si tenemos dos rectas y calculamos sus pendientes, podemos tener tres escenarios posibles, que las rectas sean paralelas, perpendiculares o simplemente tengan un ángulo diferente a 0 o 90°.
Ejemplo de paralelismo y perpendicularidad.
La recta AB pasa por los puntos A(-3,1) y B(3,5), la recta CD pasa por el punto C(-3,5) y D(1,-1), determina si las dos rectas son paralelas, perpendiculares o hay un ángulo diferente de 0° o 90°.
Lo primero que se debe hacer es calcular las pendientes de las dos rectas AB y CD
Pendiente de la recta AB
$$m_{AB}=\frac{5-1}{3-(-3)}=\frac{4}{6}$$
$$m_{AB}=\frac{2}{3}$$
Pendiente de la recta CD
$$m_{CD}=\frac{-1-5}{1-(-3)}=\frac{-6}{4}$$
$$m_{CD}=\frac{-3}{2}$$
Revisando nuestras afirmaciones, tenemos que de inicio las pendientes antes calculadas no son iguales, por lo tanto, no son paralelas y nos lleva a calcular el recíproco negativo para ver si son perpendiculares.
$$m_{AB}=\frac{-1}{m_{CD}}$$
$$m_{AB}=\frac{-1}{\frac{-3}{2}}=\frac{\frac{-1}{1}}{\frac{-3}{2}}$$
$$m_{AB}=\frac{-2}{-3}$$
$$m_{AB}=\frac{2}{3}$$
Como vemos se cumple la igualdad y por este motivo podemos afirmar que las rectas son perpendiculares.