En geometría Analítica nos encontramos muchos problemas con la medición de
ángulos entre dos rectas. Por ésta razón ponemos a continuación una figura
para entender como se mide el ángulo entre dichas rectas.
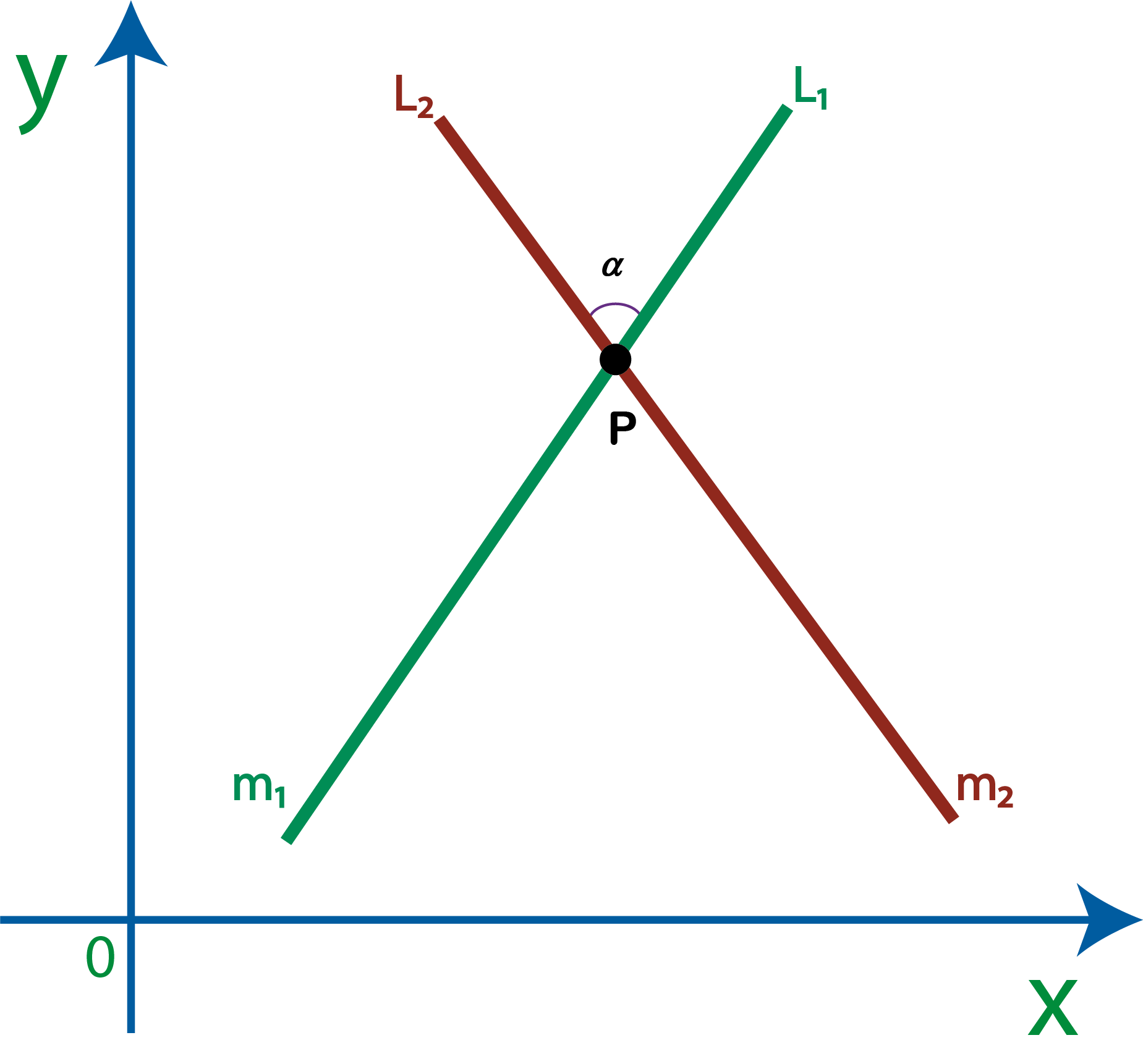
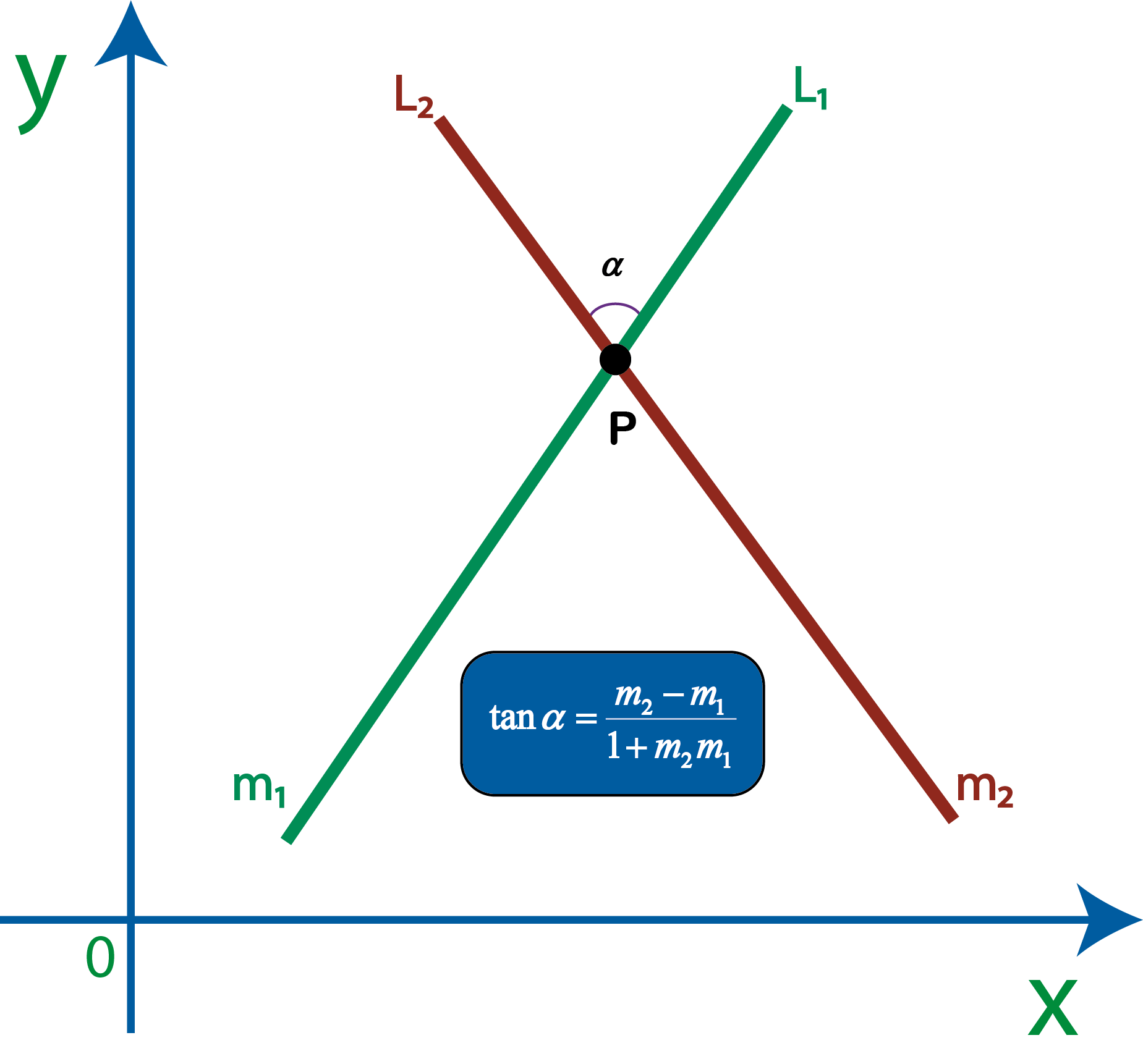
Como vemos en la figura, hay dos rectas que tienen un ángulo $\alpha$ entre ellas. Debemos identificar la recta de la izquierda y la recta de la derecha, para tal fin, debemos situarnos como si el punto P fuera un orificio por donde ver el ángulo $\alpha$, estando de esta forma el lado izquierdo quedaría donde esta la línea roja $L_2$ y el lado derecho en la línea verde $L_1$.
La fórmula que le corresponde a la magnitud del ángulo entre dos rectas es:
$$tan\;\alpha=\frac{m_{izquierda}-m_{derecha}}{1+m_{izquierda}m_{derecha}}$$
Y poniéndola referida a las pendientes $m_1$ y $m_2$ queda:
$$tan\;\alpha=\frac{m_2-m_1}{1+m_1m_2}$$
Si $1+m_1m_2=0$, entonces $\alpha=90°.$
Ángulos de un triángulo
Para saber los ángulos de un triángulo utilizaremos la fórmula anterior tres veces.
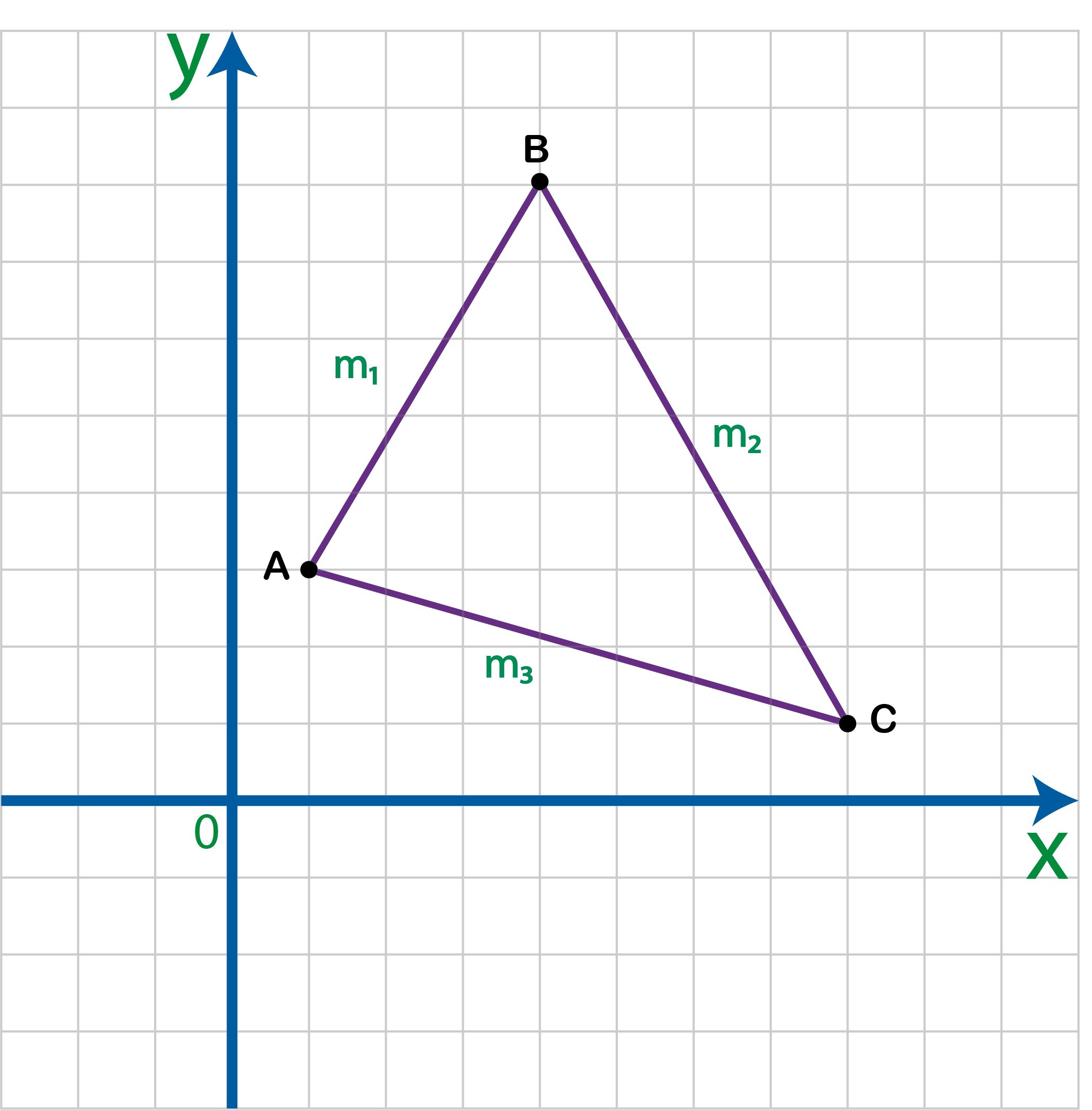
$$m_1= pendiente\; de\; \overline{AB}$$ $$m_2= pendiente\; de\;
\overline{BC}$$ $$m_3= pendiente\; de\; \overline{AC}$$
Conociendo lo anterior llegamos a las siguientes fórmulas:
Para el vértice A
$$tan\;A=\frac{m_{izquierda}-m_{derecha}}{1+m_{izquierda}m_{derecha}}=\frac{m_1-m_3}{1+m_1m_3}$$
Para el vértice B
$$tan\;B=\frac{m_{izquierda}-m_{derecha}}{1+m_{izquierda}m_{derecha}}=\frac{m_2-m_1}{1+m_2m_1}$$
Para el vértice C
$$tan\;C=\frac{m_{izquierda}-m_{derecha}}{1+m_{iquierda}m_{derecha}}=\frac{m_3-m_2}{1+m_3m_2}$$
Ejemplo de ángulo entre 2 rectas.
Hallar el ángulo entre dos rectas de acuerdo a los datos de la siguiente figura

La pendiente $m_1$ la determinamos del segmento de recta $\overline{AB}$ y
$m_2$ la determinamos del segmento de recta $\overline{CD}$.
| Pendiente de la recta $\overline{CD}$ | Pendiente de la recta $\overline{AB}$ |
| $m_2=\frac{3-5}{4-2}=\frac{-2}{2}=-1$ | $m_1=\frac{6-2}{4-2}=\frac{4}{2}=2$ |
Con lo anterior podemos obtener el ángulo $\alpha$ entre la recta 1 y la recta 2, sabiendo que $m_1$ está a la derecha y $m_2$ se encuentra a la izquierda.
$$tan\;\alpha=\frac{m_{izquierda}-m_{derecha}}{1+m_{izquierda}m_{derecha}}=\frac{-1-2}{1+(-1)(2)}$$
$$tan\;\alpha=\frac{-3}{1+(-2)}=\frac{-3}{-1}=3$$
$$\alpha=tan^{-1}(3)=71.56°$$
$$\alpha=71.56°$$