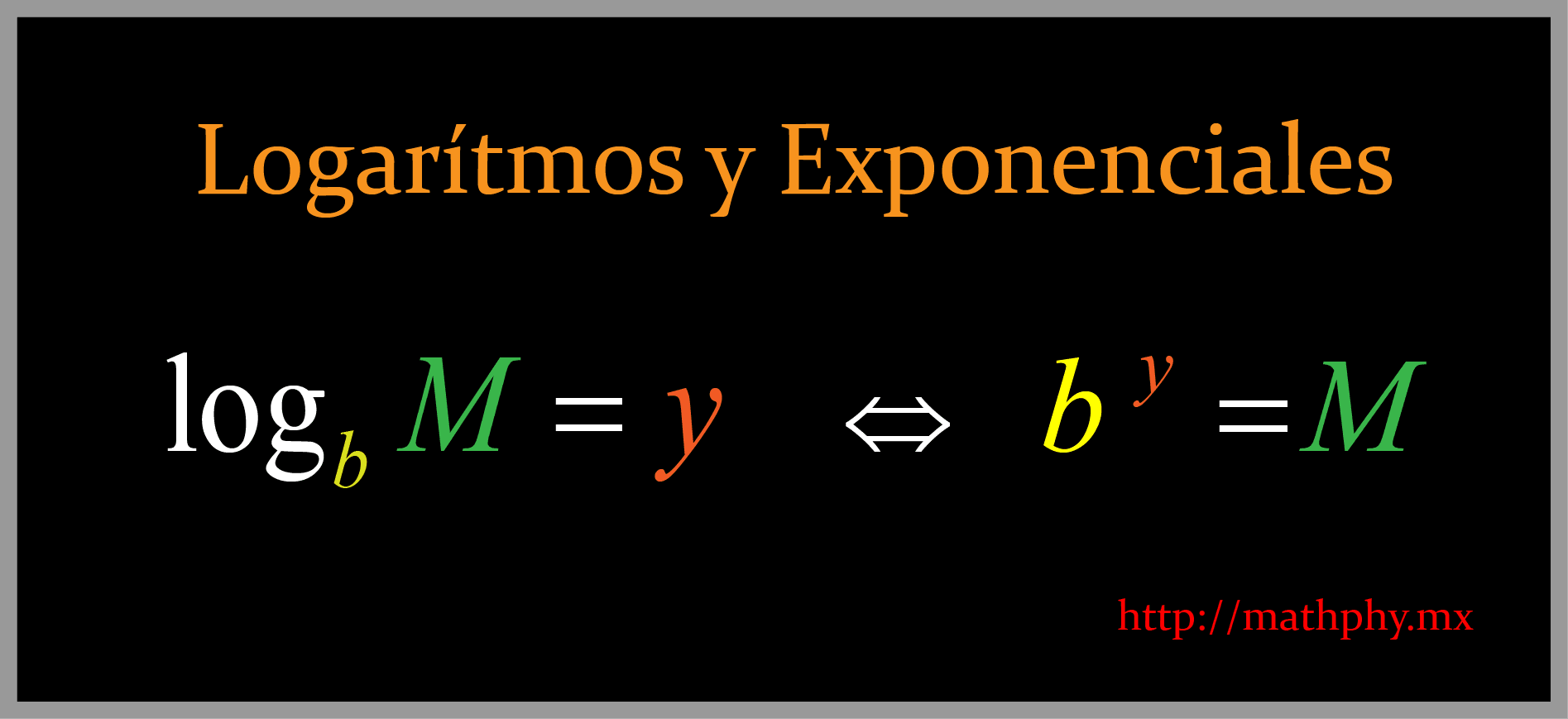El logaritmo es un exponente al cual hay que elevar una cantidad positiva para que dé un número determinado.
A continuación vemos como se transforma una función logarítmica a exponencial.
Vamos a encontrar una muy fuerte relación entre las funciones exponenciales y logarítmicas, dado que si queremos resolver una función logarítmica tenemos que
recurrir a una función exponencial y viceversa.
Propiedades de los logarítmos.
$$1. \;log_b \;xy=log_b \;x+log_b \;y$$
$$2. \;log_b \;\frac{x}{y}=log_b \;x-log_b \;y$$
$$3. \;log_b \;x^n=n\;log\;x$$
Para calcular el logarítmo de cualquier base tenenos la fórmula:
$$log_a \;x=\frac{log_b\;x}{log_b\;a}$$
Ejemplo de cambio de base
Cambiar la base del siguiente logaritmo
$$log_2\;5=\frac{log\;5}{log\;2}=\frac{ln\;5}{ln\;2}\approx2.322$$