Sabemos que una recta se forma a partir de mínimo dos puntos y que dependiendo de esos puntos podremos ver su inclinación, pero no siempre una recta se grafica, por tal motivo es necesario revisar los conceptos de pendiente e inclinación , primero de forma gráfica y después de forma analítica.
La siguiente gráfica nos muestra los elementos necesarios de una recta y para poder entender el concepto de Pendiente.
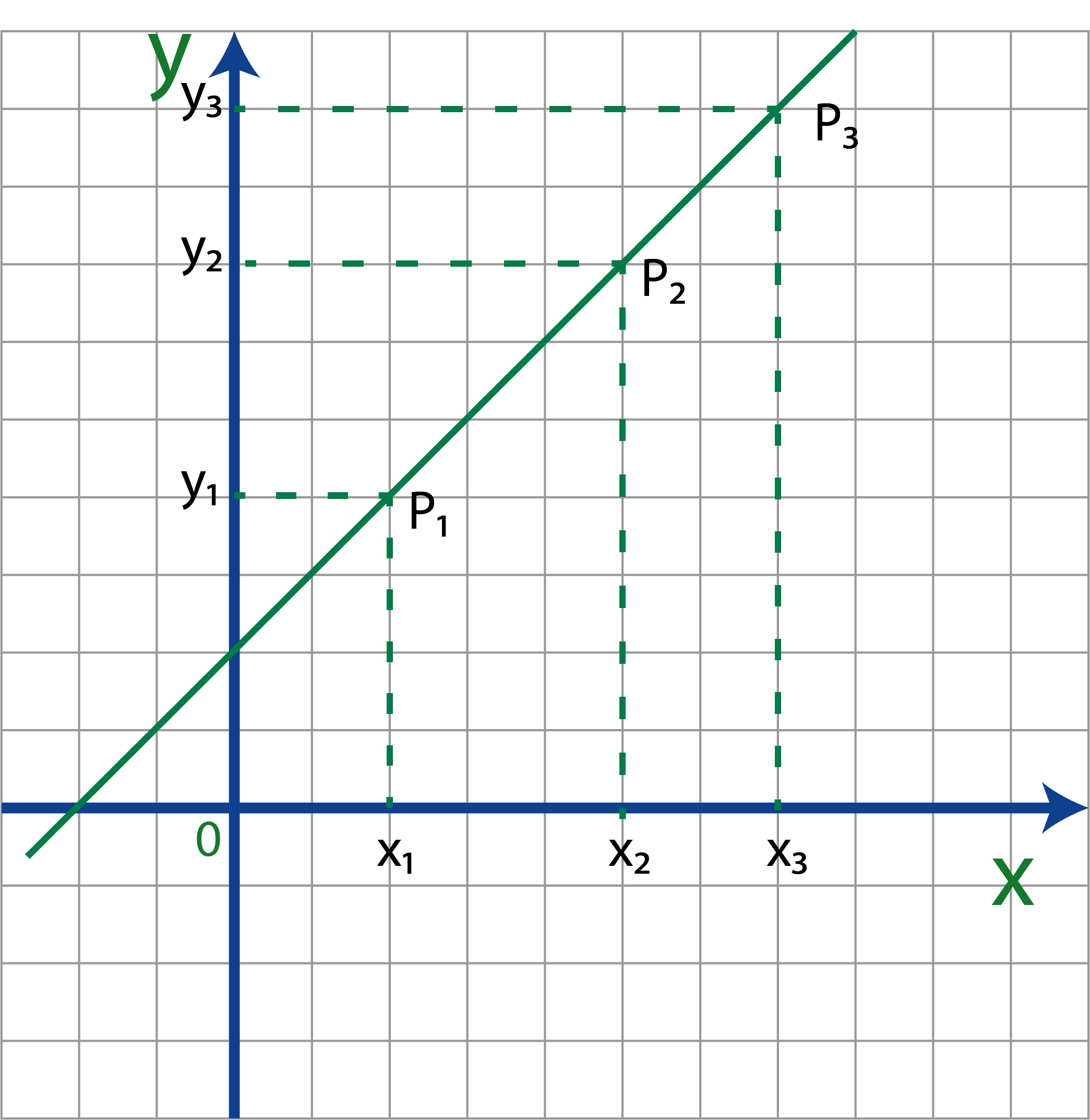
De la figura anterior podemos ver que con solo dos puntos se puede graficar una línea recta y que si definimos a la pendiente como la razón entre el recorrido de y sobre el recorrido de x de un punto a otro tenemos lo siguiente:
$$pendiente=\frac{y_2-y_1}{x_2-x_1}=\frac{y_3-y_2}{x_3-x_2}$$
Se denota a la pendiente con la letra m (contracción de “mutatio -nis” cuyo significado en latín es: cambio), por lo tanto para tener una fórmula de ella, tenemos:
$$m=\frac{y_2-y_1}{x_2-x_1}$$
Se tienen diferentes formas de pendientes, eso dependerá de sus puntos extremos, pero veremos a continuación algunas formas de pendiente de acuerdo a su signo o valor.
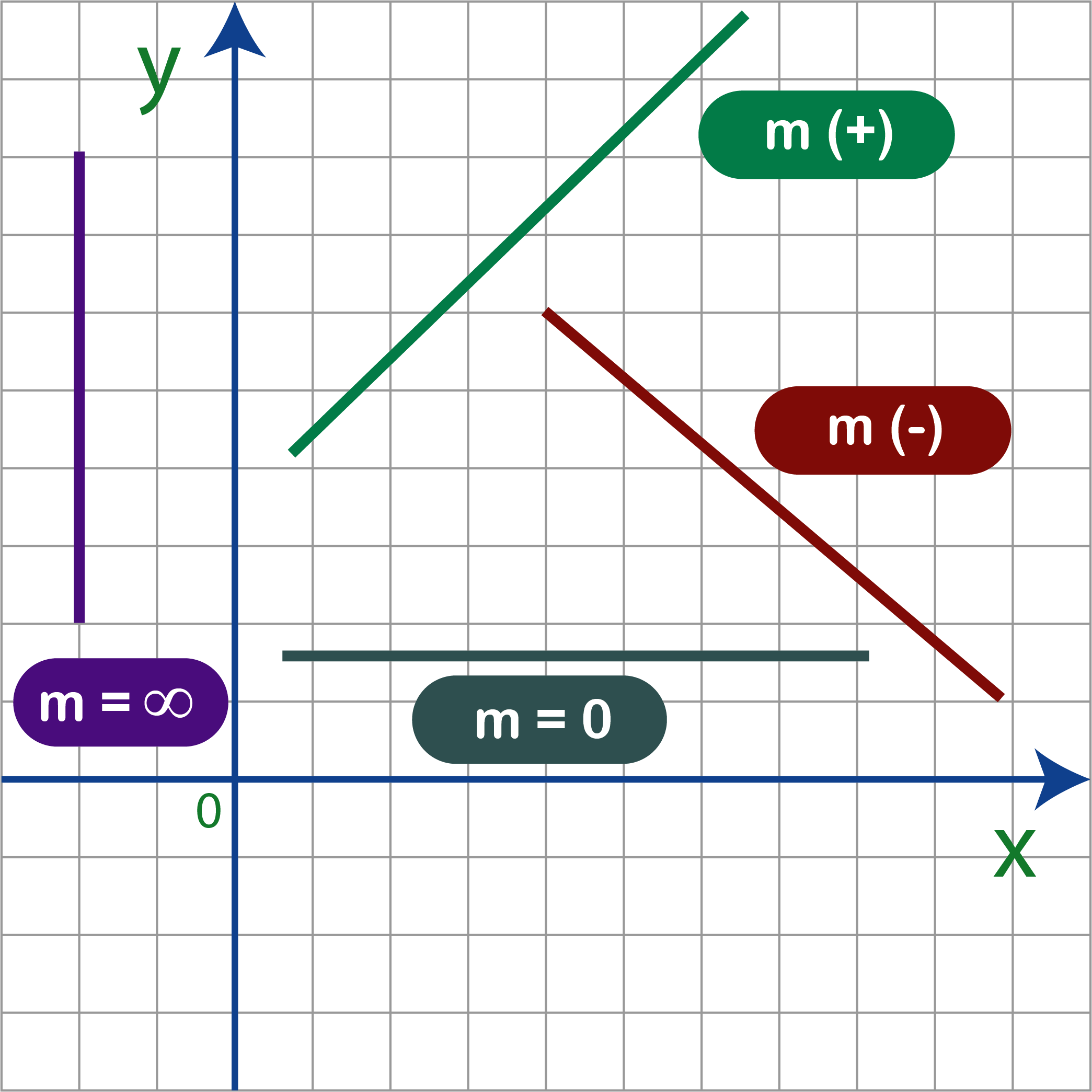
| Para el caso en que m = + la pendiente es ascendente de izquierda a derecha. |
| Para el caso en que m = – la pendiente es descendente de izquierda a derecha. |
| Para el caso en que m = 0 la pendiente es nula o simplemente no hay pendiente y está de forma horizontal. |
| Para el caso en que $m=\infty$ no hay pendiente o no existe y se encontrará de forma vertical. |
Inclinación de una recta.
Por otra parte definimos la inclinación como el ángulo no negativo que se tiene desde el eje x positivo hasta la recta.
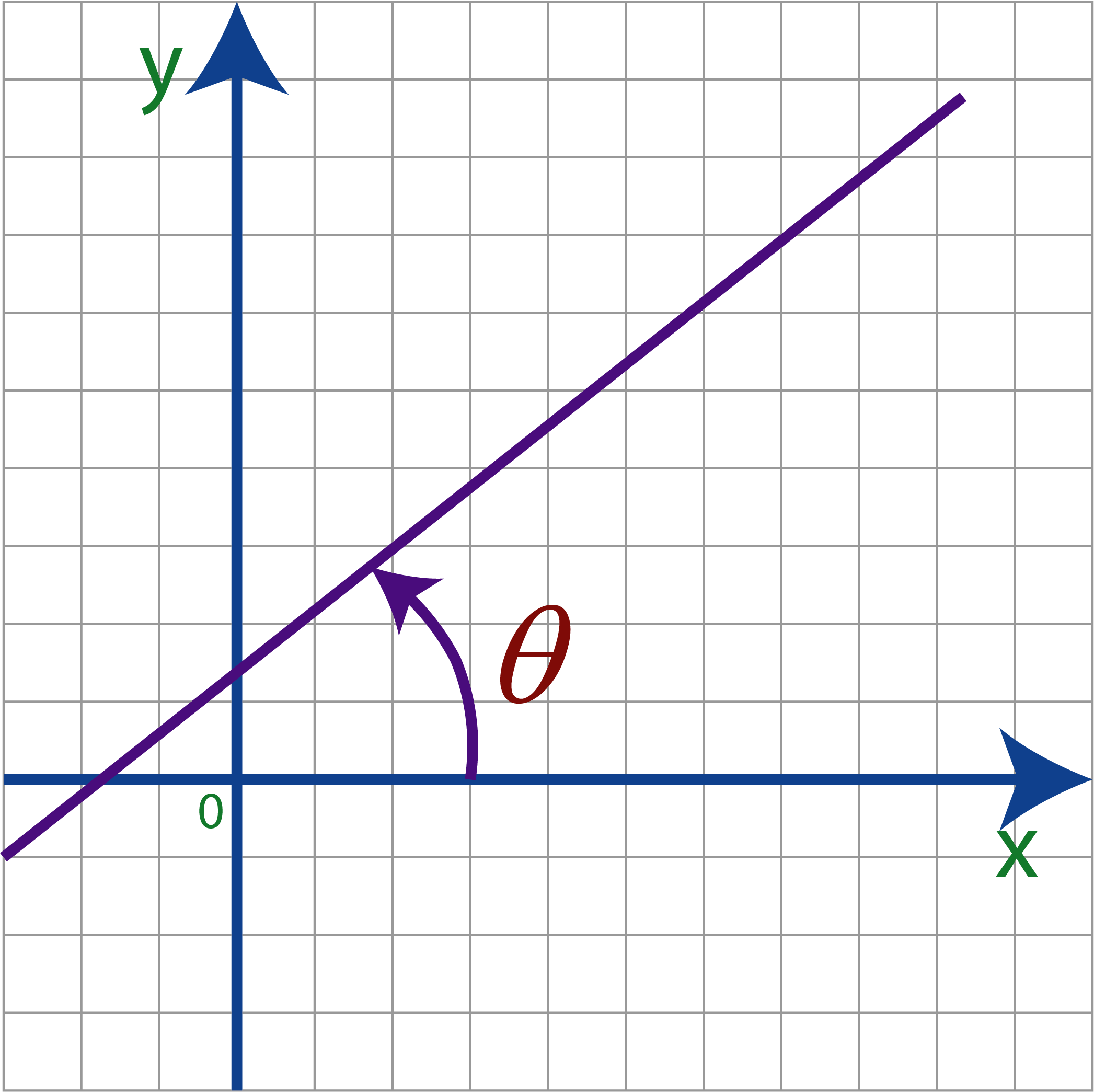
El ángulo positivo se tiene cuando su dirección de recorrido es en sentido contrario de la manecillas del reloj de otra forma será un ángulo negativo.
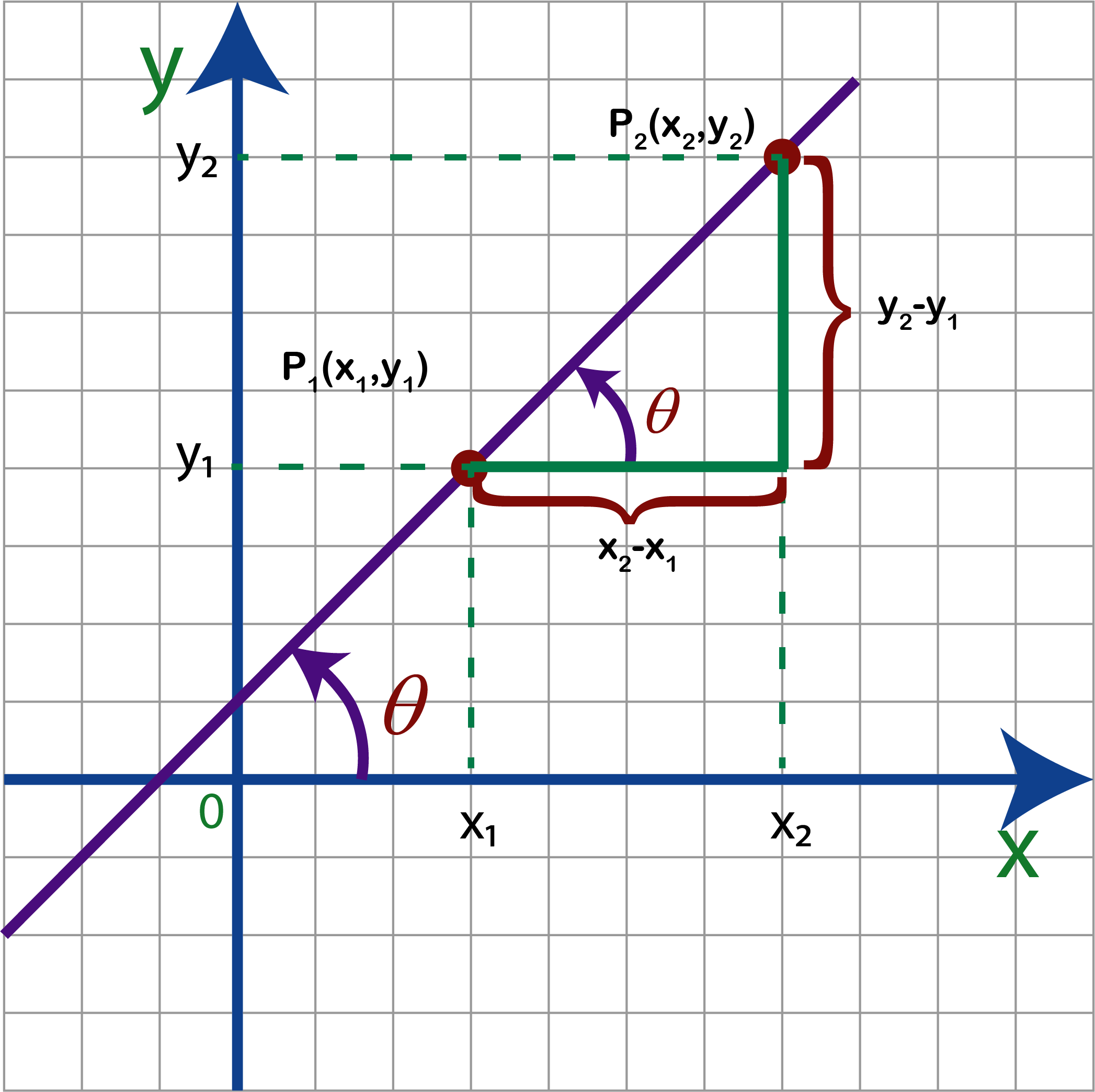
Para deducir la inclinación vemos en la figura anterior que la recta se comporta como una hipotenusa de un triángulo rectángulo y sus catetos como los lados, de el concepto de triángulo rectángulo tenemos que la tangente del ángulo $\theta$ es igual a cateto opuesto sobre cateto adyacente, quedando la fórmula como sigue:
$$tan\;\theta=\frac{y_2-y_1}{x_2-x_1}=m$$
Así se ve claramente que la pendiente es igual a la tangente del ángulo de inclinación:
$$tan\;\theta=m$$
$$\theta=tan^{-1}\;m$$
Primero calculamos la pendiente con los puntos A y B.
$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{5-15}{15-(-5)}$$
$$m=\frac{-10}{20}=\frac{-1}{2}$$
$$m=\frac{-1}{2}$$
El valor anterior es la pendiente, ahora nos toca resolver la inclinación.
La fórmula de inclinación es la siguiente:
$$tan\;\theta =m$$
$$\theta =tan^{-1}\;m$$
$$\theta =tan^{-1}\;\left(\frac{-1}{2}\right)=-26.56°$$
El ángulo es negativo, para volverlo positivo hacemos lo siguiente:
$$\theta_+=180°-26.56°$$
$$\theta_+=153.43°$$

