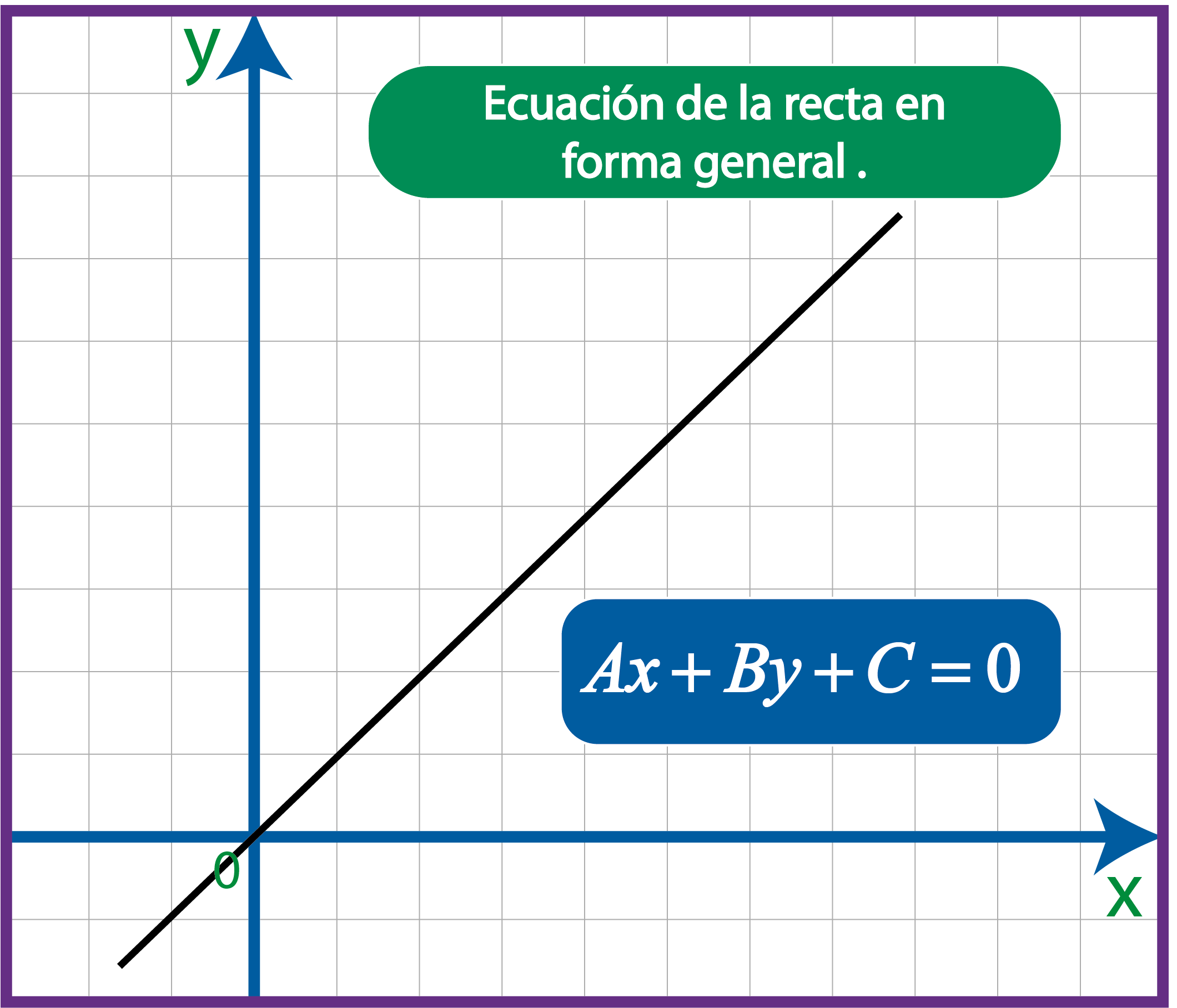
La ecuación de la recta en forma general nos proporciona información importante, su forma es la $Ax+By+C=0$ y dependiendo los valores de A, B y C, se sabrá si pasa por el origen, es paralela al eje x o y, etc. Recordar que A y B no puede valer cero simultáneamente.
Vamos a revisar tres diferentes casos donde la ecuación de la recta en forma general está incompleta.
Caso 1. Cuando la letra C es igual a cero, queda de la siguiente forma $Ax+By=0$ y como se ve, que para que se cumpla la igualdad, forzosamente $x=0$ y $y=0$ para cumplir con la igualdad a cero. Por lo tanto, la ecuación representa una gráfica que pasa por el origen.
Caso 2. Cuando la letra $A\neq0$ y $B=0$ , queda de la siguiente forma $Ax+C=0$, representa una gráfica paralela al eje y, donde $x=h$, siendo $h=-\frac{C}{A}$. Si el valor de $h=0$, la recta coincide con el eje y, por lo tanto, $x=0$ es el eje y en toda su extensión.
Caso 3. Cuando la letra $A=0$ y $B\neq0$ , queda de la siguiente forma $By+C=0$, representa una gráfica paralela al eje x, donde $y=k$, siendo $k=-\frac{C}{B}$. Si el valor de $k=0$, la recta coincide con el eje x, por lo tanto, $y=0$ es el eje x en toda su extensión.
Ejemplo de la ecuación de la recta en forma general.
Determina la ecuación de la recta que pasa por el punto A(3,5) y tiene como pendiente el valor de 5.
Utilizamos la ecuación punto pendiente.
$$(y-y_1)=m(x-x_1)$$
$$(y-5)=5(x-3)$$
Desarrollamos la ecuación y pasamos todo del lado izquierdo , para que quede igualado a cero.
$$y-5=5x-15 \;\; \Rightarrow \;\;-5x+y=-15+5$$
$$-5x+y=-10$$
Multiplicando ambos lados por -1:
$$5x-y=10$$
Dejando todo los elementos del lado izquierdo, por lo tanto queda igualado a cero del lado derecho
La ecuación anterior representa la ecuación en forma general de la recta.
Recordar que hasta el momento hemos visto 4 formatos de ecuación, por lo que se pueden transformar de uno hacia otro mediante álgebra.