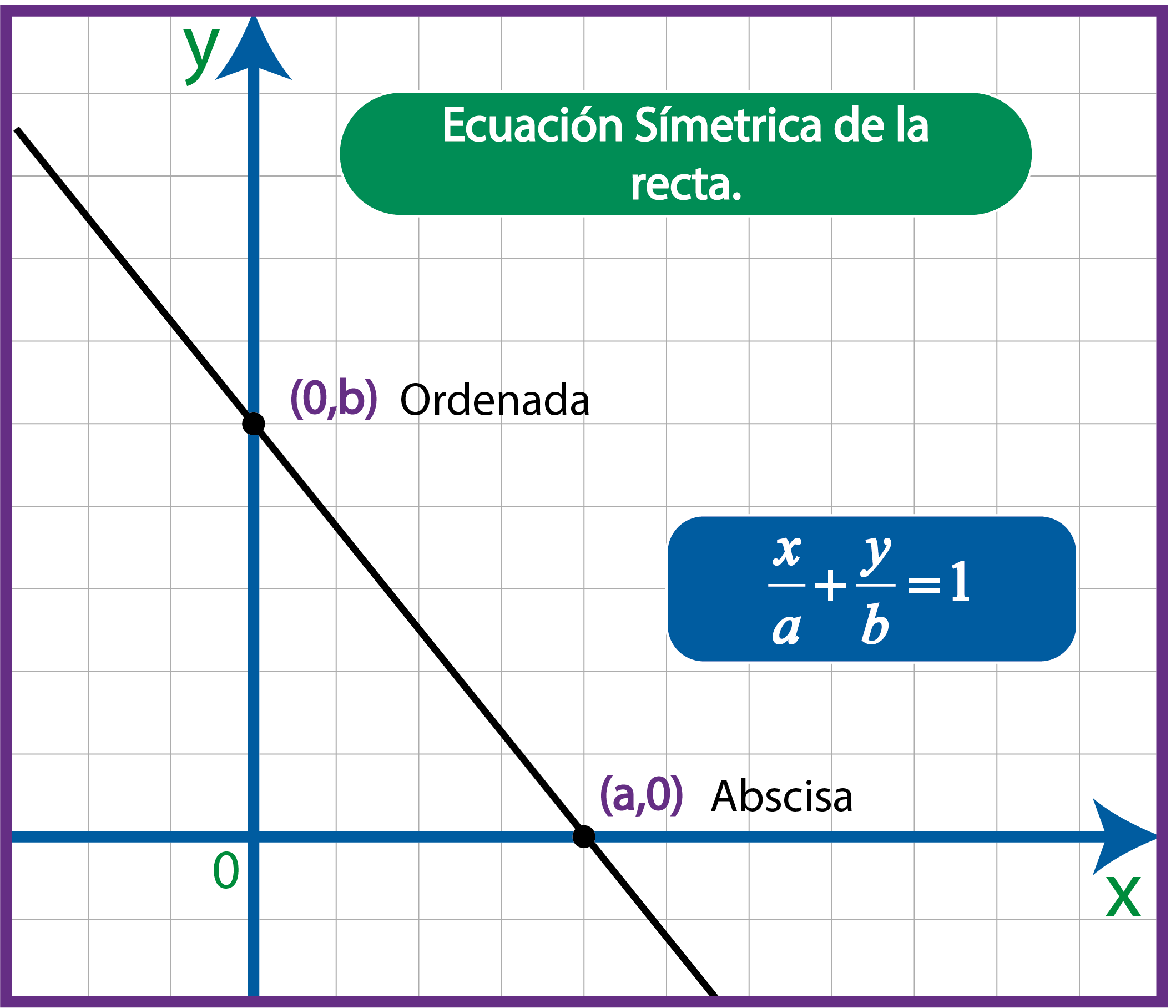
La línea recta tiene una ecuación en forma simétrica que conlleva los valores de a y b, los cuales corresponden a los valores de la abscisa y la ordenada. Dicha información es importante para poder de un lado graficar la ecuación de manera más rápido, porque nos ofrece dos puntos conocidos y por otro lado al saber el punto donde corta el eje x, se sabe la raíz de la ecuación.
La ecuación en forma simétrica queda de la siguiente forma:
El valor de a es la abscisa en el origen de la recta
El valor de b es la ordenada en el origen de la recta
Ejemplo de Línea Recta. Ecuación en forma simétrica.
Determinar la ecuación de la recta en forma simétrica que pasa por los puntos A(-3,4) y B(6,-2). Grafica la recta.
Primero debemos determinar la ecuación de la recta en forma punto pendiente, para tal caso utilizaremos la siguiente ecuación:
$$(y-y_1)=m\;(x-x_1)$$
Siendo $x_1=-3\;, y_1=4$ y $x_2=6\;, y_2=-2$, los sustituimos dentro de la ecuación de pendiente.
$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{-2-4}{6-(-3)}$$
$$m=\frac{-6}{6+3}=\frac{-6}{9}=\frac{-2}{3}$$
$$m=\frac{-2}{3}$$
Sustituyendo la pendiente en la ecuación punto pendiente, tenemos:
$$(y-4)=\frac{-2}{3}\;(x-(-3))$$
$$(y-4)=\frac{-2}{3}\;(x+3)$$
Desarrollando la ecuación anterior:
$$3(y-4)=-2\;(x+3)$$
$$3y-12=-2x-6$$
Pasando las variables del lado izquierdo y los números del lado derecho.
$$2x +3y=-6+12$$
$$2x +3y=6$$
Dividiendo el lado derecho e izquierdo entre 6, para que el lado derecho se transforme en 1
$$\frac{2x +3y}{6}=\frac{6}{6}$$
Separando las fracciones:
$$\frac{2x}{6}+\frac{3y}{6}=1$$
Haciendo la reducción de las fracciones, queda:
$$\frac{\frac{2x}{2}}{\frac{6}{2}}+\frac{\frac{3y}{3}}{\frac{6}{3}}=1$$
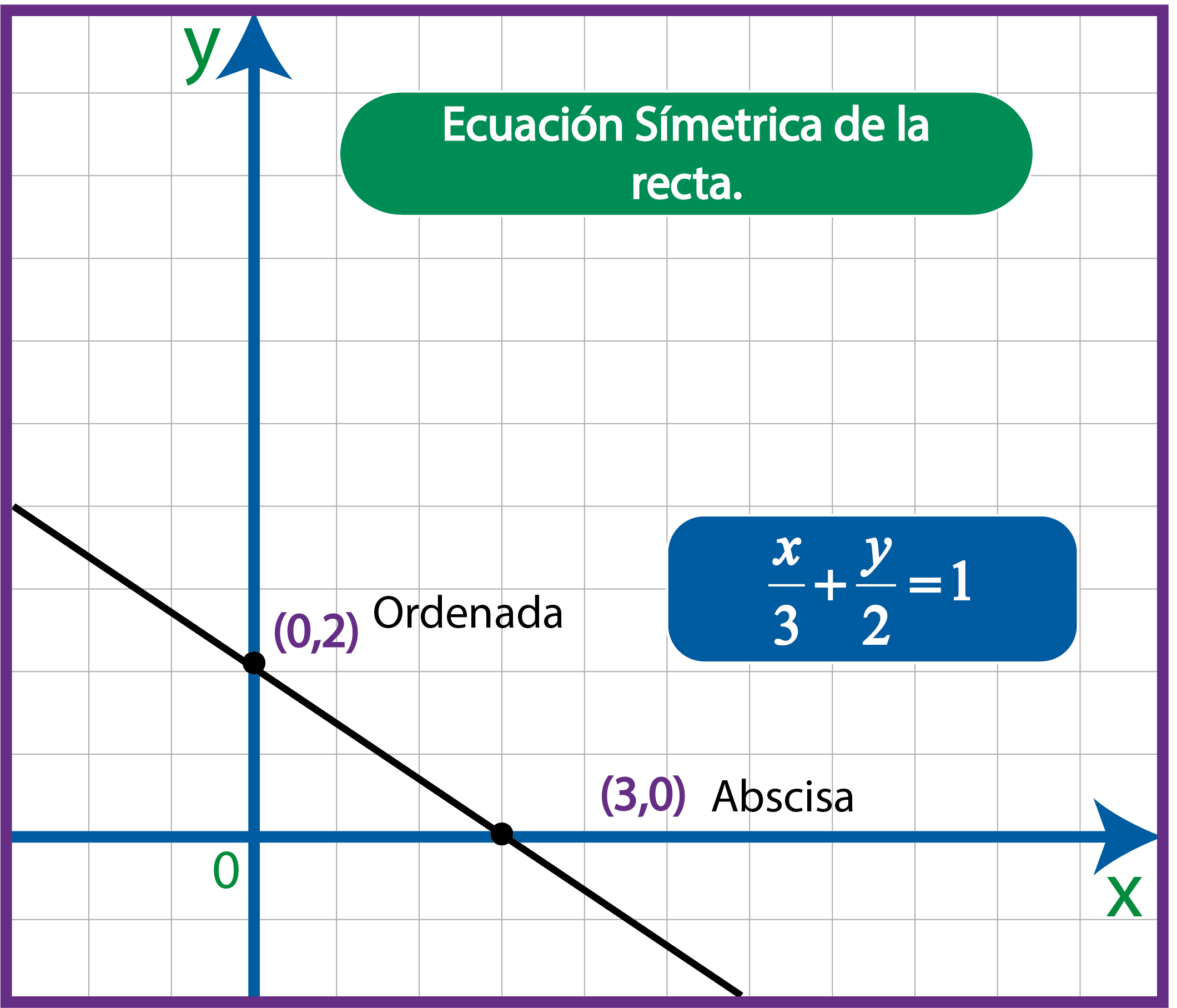
$$\frac{x}{3}+\frac{y}{2}=1$$
Ecuación de la recta en forma simétrica .
Vemos que la abscisa vale 3 y la ordenada vale 2, con esos datos podemos graficar la recta.