Línea Recta. Ecuación Pendiente Ordenada al Origen.

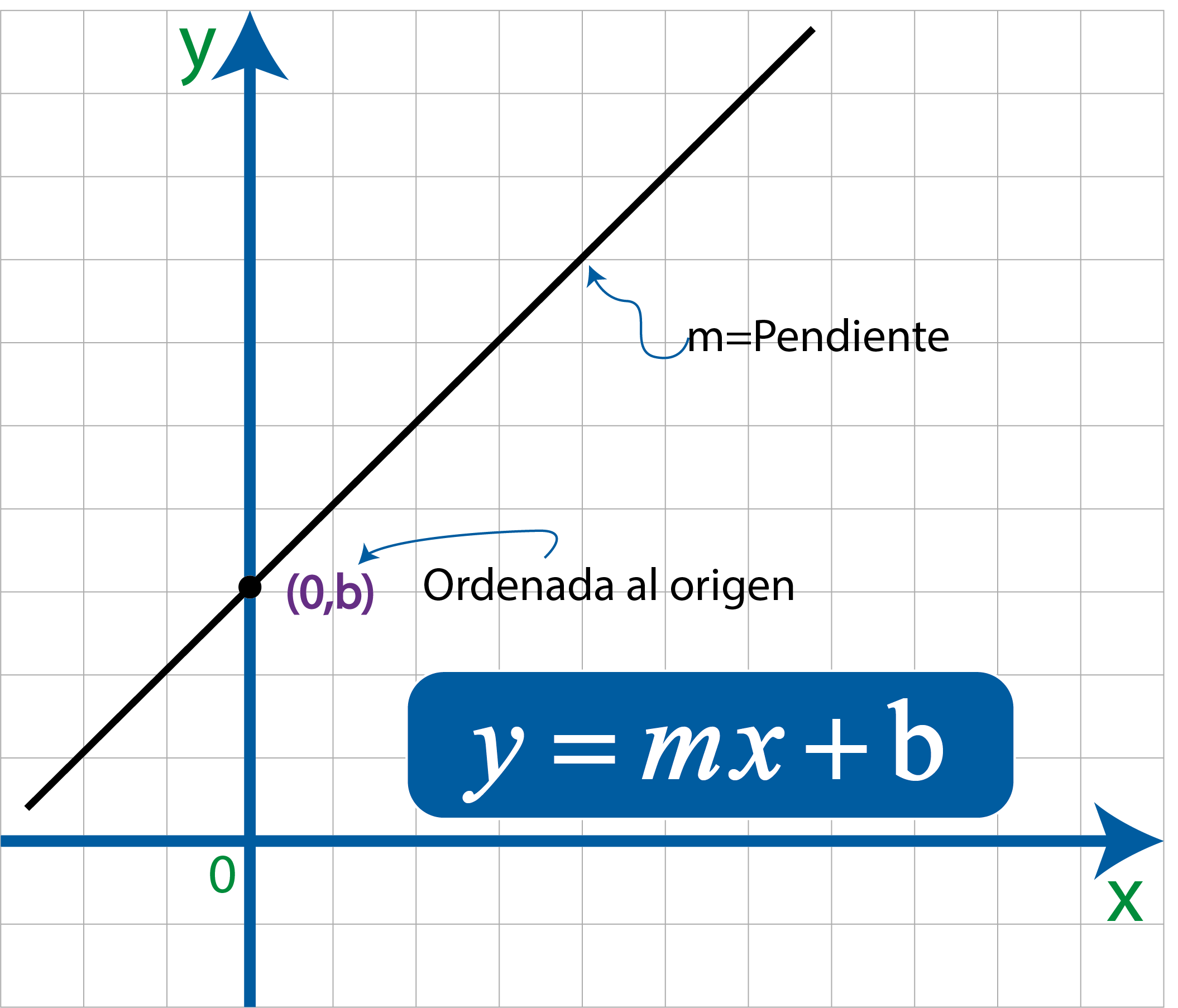
La ecuación de la recta en forma pendiente ordenada al origen nos proporciona dos datos fundamentales en una recta. Los datos son su pendiente y por donde cruza la recta el eje y.

Es importante mencionar que la ecuación en forma pendiente ordenada al origen es común encontrarla en la literatura matemática.

Como se puede ver en la figura anterior, para encontrar la ecuación pendiente orde nada al origen debemos saber la el valor de la pendiente y la ordenada al origen (b).La la ecuación queda de la siguiente forma:

Ejemplo de Línea Recta. Ecuación Pendiente Ordenada al Origen.

Determina la ecuación de la recta que pasa por los puntos A(4,-2) y B(6,4).

Lo primero que se debe de hacer es calcular el valor de la pendiente de la recta entre el punto A y B.

$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{4-(-2)}{6-4}$$
$$m=\frac{4+2}{2}=\frac{6}{2}=3$$

Como no tenemos el valor de b debemos realizar el problema como si fuera encontrar la ecuación punto pendiente , para lo cual necesitaremos la siguiente ecuación:

$$(y-y_1)=m\;(x-x_1)$$

Sustituyendo los valores, obtenemos lo siguiente:

$$(y-(-2))=3\;(x-4)$$
$$(y+2)=3\;(x-4)$$

y de la ecuación anterior despejamos la letra y.

$$(y+2)=3\;(x-4)$$
$$y+2=3x-12$$
$$y=3x-12-2$$
$$y=3x-14$$