La ecuación de la línea recta tiene muchas variantes, en nuestro caso veremos 5 diferentes formas y las mencionaremos a continuación:
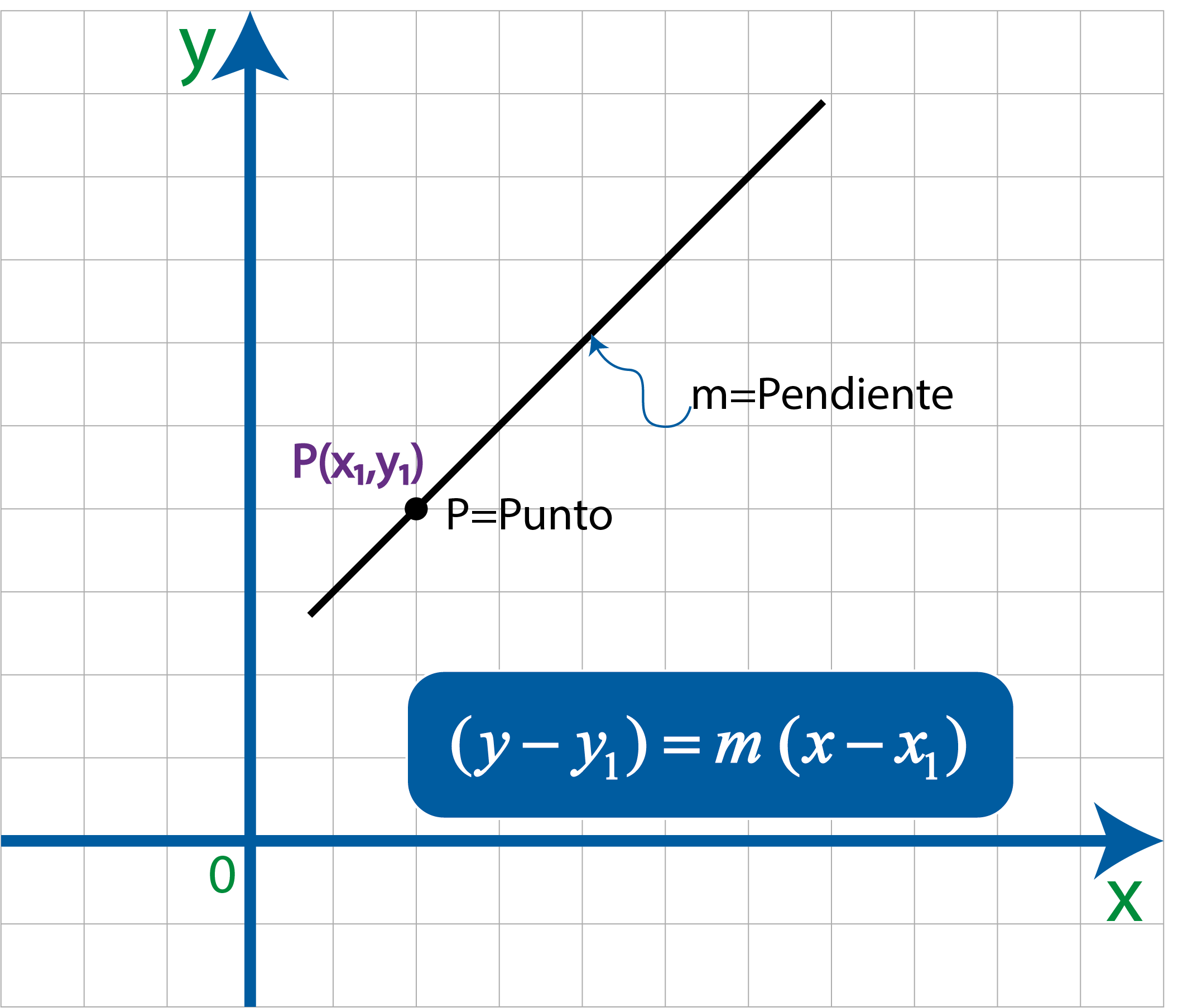
La primera forma a estudiar será la ecuación punto pendiente, dado que solo necesitamos el valor de la pendiente y un punto para determinar dicha ecuación.
Para determinar esta ecuación, solo debemos saber los valores de $P(x_1,y_1)$ y la pendiente $m$.La fórmula queda de la siguiente forma:
Ejercicio de la Línea Recta. Ecuación Punto Pendiente.
Determinar la ecuación punto pendiente de la recta que pasa por los puntos A(-2,5) y B(4,-1).
La recta no proporciona la pendiente, solo dos puntos, por lo tanto se debe calcular la pendiente y utilizar el primer punto en la ecuación punto pendiente de la recta.
Cálculo de la pendiente.
Para determinar el valor de la pendiente, se tiene que sustituir el valor de los puntos A y B en la fórmula de pendiente $m=\frac{y_2-y_1}{x_2-x_1}$.
$$m=\frac{y_2-y_1}{x_2-x_1}=\frac{-1-5}{4-(-2)}$$
$$m=\frac{-6}{4+2}=\frac{-6}{6}=-1$$
Sabiendo la pendiente y tomando el punto A(-2,5) como el punto conocido o punto $P(x_1,y_1)$, podemos encontrar la ecuación punto pendiente.
$$(y-y_1)=m\;(x-x_1)$$
$$(y-5)=-1\;(x-(-2))$$
$$(y-5)=-(x+2)$$
Ecuación Punto Pendiente de la Recta.